Пространственная автокорреляция
1 Теория
Материалы лекции
Открыть лекцию в новой вкладке
Материалы лекции (eng.)
2 Пространственный лаг
Пространственный лаг - это взвешенная сумма значений для каждого из объектов. Так как веса задаются матрицей пространственных весов, то пространственный лаг фактически описывает окружение каждого объекта.
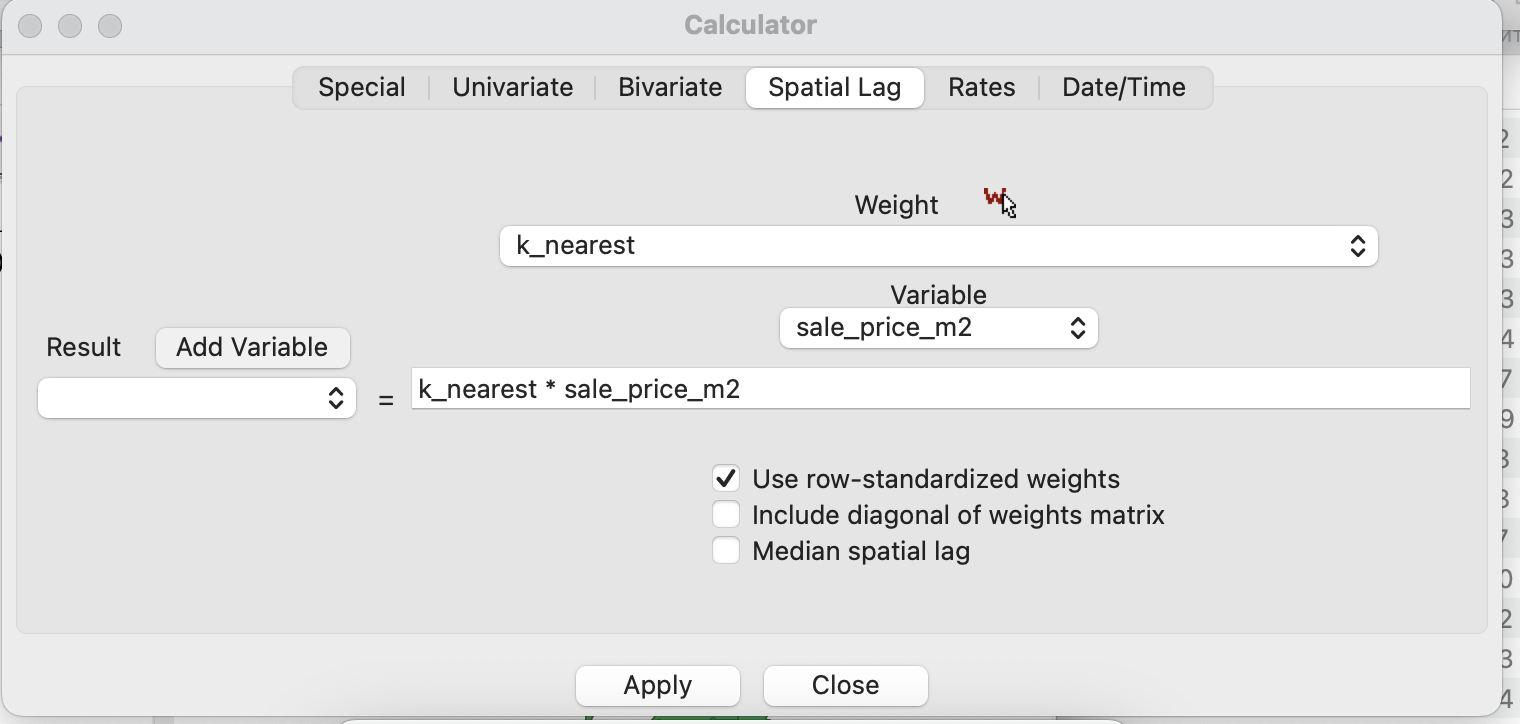
Вычисление пространственного лага осуществляется с использованием калькулятора.
Если по результатам прошлого занятия вы не сохранили себе данные как проект и у вас нет весовых матриц, вы можете просто загрузить их в менеджере весов.
В том случае, если идентификаторы для матрицы весов пропали, вы можете просто добавить их заново аналогично тому, как мы добавляли их в прошлый раз.
Для его вычисления необходимо указать:
используемую матрицу весов (если у вас их несколько, то может быть выбрана одна из них);
переменную, для которой осуществляется вычисление лага (здесь может быть выбрана любая количественная переменная из вашей атрибутивной таблицы);
переменную для записи результата - здесь может быть выбрана существующая колонка или создана новая.
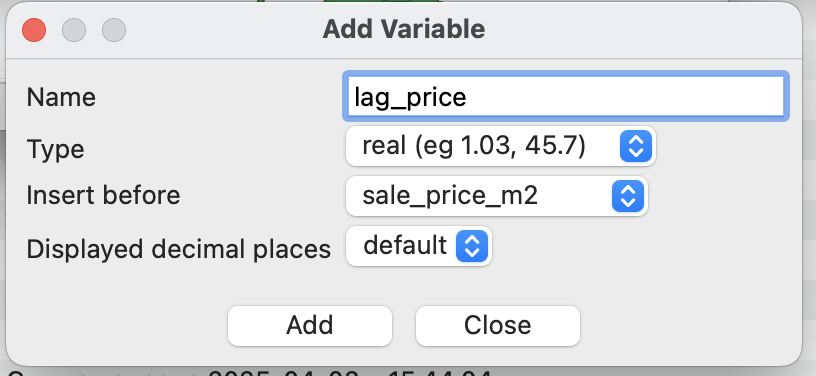
В качестве дополнительный опций вы можете указать необходимость стандартизации весов по строкам матрицы, включение диагональных элементов (фактически определяет включение значение для самого объекта в пространственный лаг).
Рекомендуется использовать стандартизованные веса для того, чтобы избежать значительных выбросов и получить более сглаженные значения.
В результате вы получите новую переменную, которая будет содержать в себе значения пространственного лага, то есть значения исследуемой переменной в окружении каждого объекта.
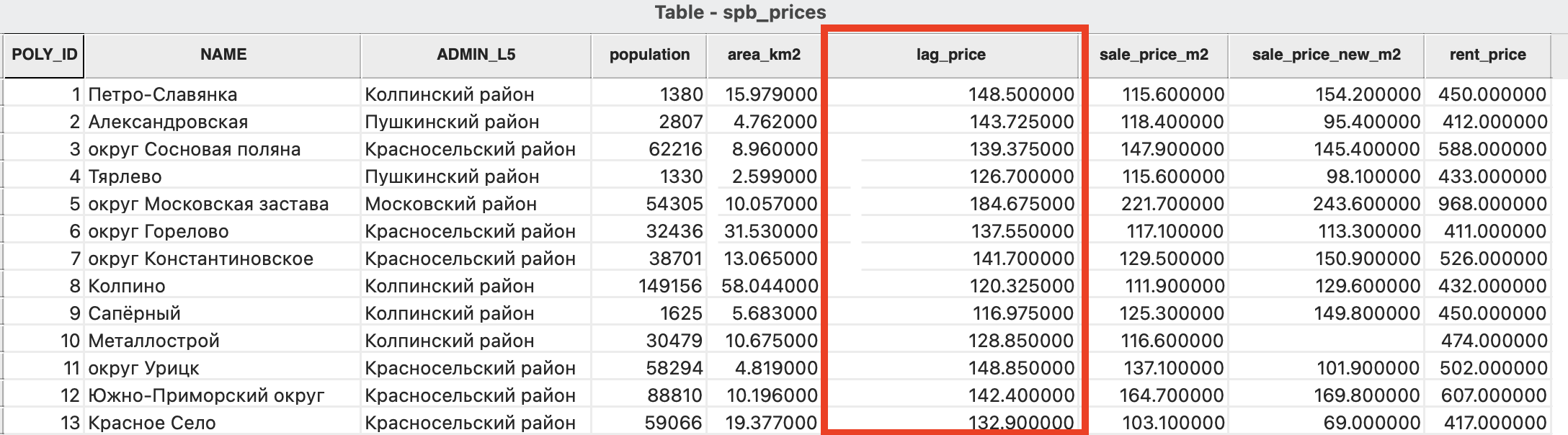
Попробуйте рассчитать пространственный лаг с использованием разных матриц весов и сравнить полученный результат.
3 Глобальная пространственная автокорреляция
Глобальная пространственная автокорреляция позволяет выявить наличие связи значений объектов друг с другом.
Процесс тестирования на наличие пространственной автокорреляции по этапам:
1. нулевая и альтернативная гипотезы \(H_0: I = E[I]\) (пространственная случайность) и \(H_1: I \neq E[I]\) (наличие пространственной автокорреляции);
2. установление уровня значимости \(\alpha\) (как правило, стандартным уровнем значимости является \(\alpha=0,05\));
3. вычисление статистики тестирования \(z = \frac{I-E(I)}{Var(I)^{1/2}}\), где \(Var[I] = \frac{n^2(n-1)S_1 - n(n-1)S_2 - 2 S_0^2}{(n+1)(n-1)^2 S_0^2}\) , \(S_0 = \sum_{i \neq j} w_{ij},\ S_1= \frac{1}{2}\sum_{i\neq j} (w_{ij}+w_{ji})^2\) и \(S_2 = \sum_k \left(\sum_j w_{kj}+\sum_i w_{ik}\right)^2\);
4. определить \(p\) - значение (либо с использованием нормального распределения, либо с использованием рандомизации по методу Монте-Карло);
5. определение наличия (\(p\) - значение \(< \alpha\)) или отсутствия (\(p\) - значение \(\geq \alpha\)) пространственной автокорреляции.
Расчет глобальных индексов простанственной автокорреляции может быть осуществлен либо инструментом (Moran scatter plot) ![]() , либо с использованием пункта Space строки меню (здесь на данном этапе вас интересуют только пункты, перечисленные до первой горизонтальной черты).
, либо с использованием пункта Space строки меню (здесь на данном этапе вас интересуют только пункты, перечисленные до первой горизонтальной черты).
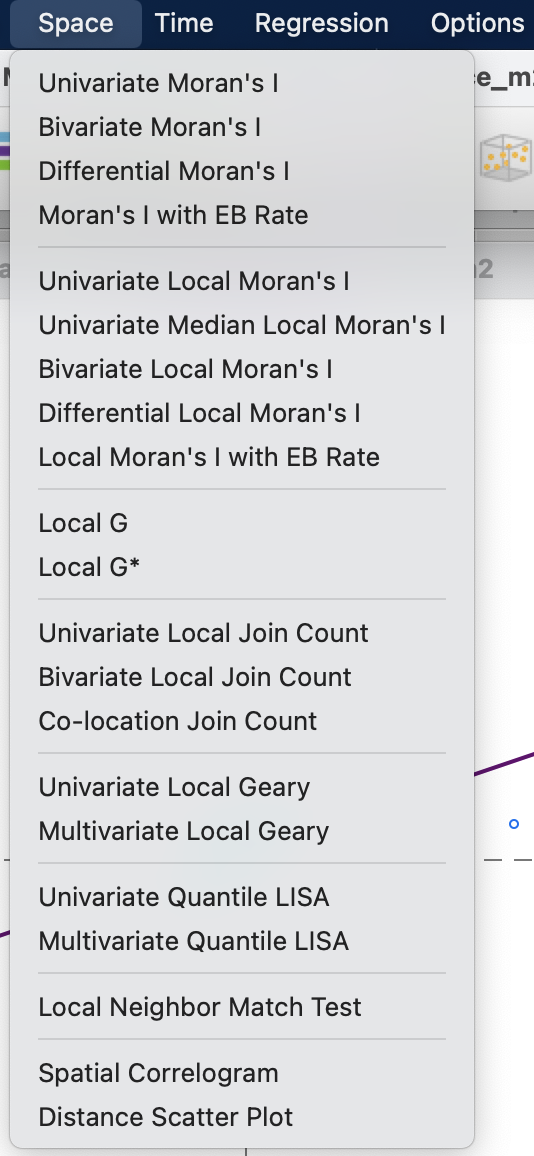
При использовании инструмента напрямую из панели, вы увидите выбор их нескольких вариаций коэффицента пространственной автокорреляции - индекса Морана I:
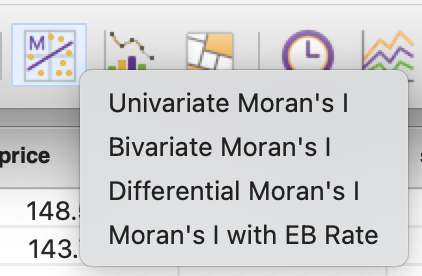
вычисление индекса по одной переменной - Univariate Moran’s I;
высисление индекса по двум переменным (для второй из них используется на само значение, а величина пространственного лага) - Bivariate Moran’s I;
дифференциальный индекс, позволяющий выявлять временные изменения в переменной (подробнее здесь) - Differential Moran’s I;
байесовский эмпирический индекс - Moran’s I with EB rate.
Мы с вами будем рассчитывать только индекс Морана для одной переменной.
В качестве параметров для расчета необходимо указать используемую переменную и матрицу весов.
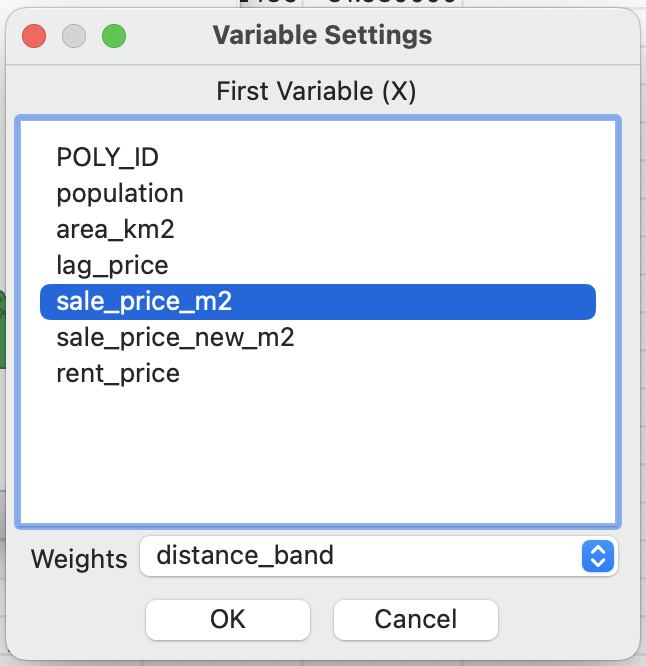
По результататм расчета вы получите график Морана в отдельном окне.
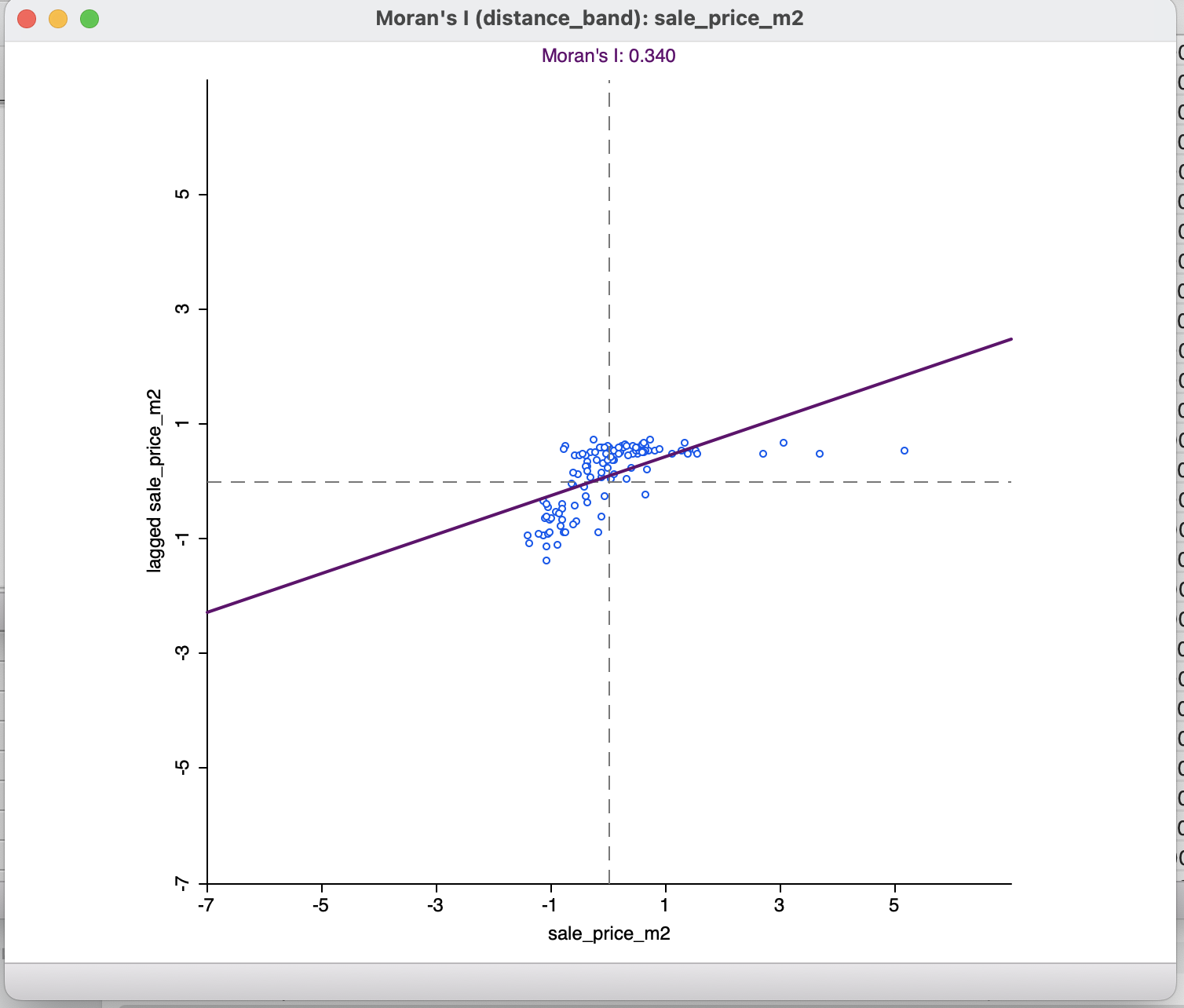
По оси \(X\) графика отображается значение самой переменной, а по оси \(Y\) - пространственный лаг этой переменной. Обе эти переменные нормализованы для того, чтобы график был более легко интерпретируемым. Поэтому ноли графика - это не нулевые значения, а средние.
Над графиком показано значение индекса Морана для исследуемой переменной и использованной матрицы весов.
По углу наклона прямой на графике и значению индекса Морана мы получаем положительную пространственную автокорреляцию, то есть объекты с близким значением переменной будут располагаться рядом друг с другом.
Значение индекса Морана будет варьироваться в зависимости от выбора матрицы весов даже, если вы используете одну и ту же переменную.
Для проверки статистической значимости индекса Морана используется метод Монте-Карло, то есть выполняется случайная перестановка данных заданное количество раз и рассчитывается коэффициент пространственной автокорреляции. Полученные результаты формируют график распределения значения индекса Морана и сравниваются с фактическим значением.
Запуск процесса проверки на статистическую значимость осуществляется по клику правой кнопки мыши на пустом пространстве графика Морана.
На представленном ниже графике бордовым показан график распределения значений индекса Морана по результатам случайных перестановок, а зеленым столбцом - фактическое значение. В верхней части окна приведена величина уровня значимости, а отдельные рассчитанные значения статистической значимости под графиком.
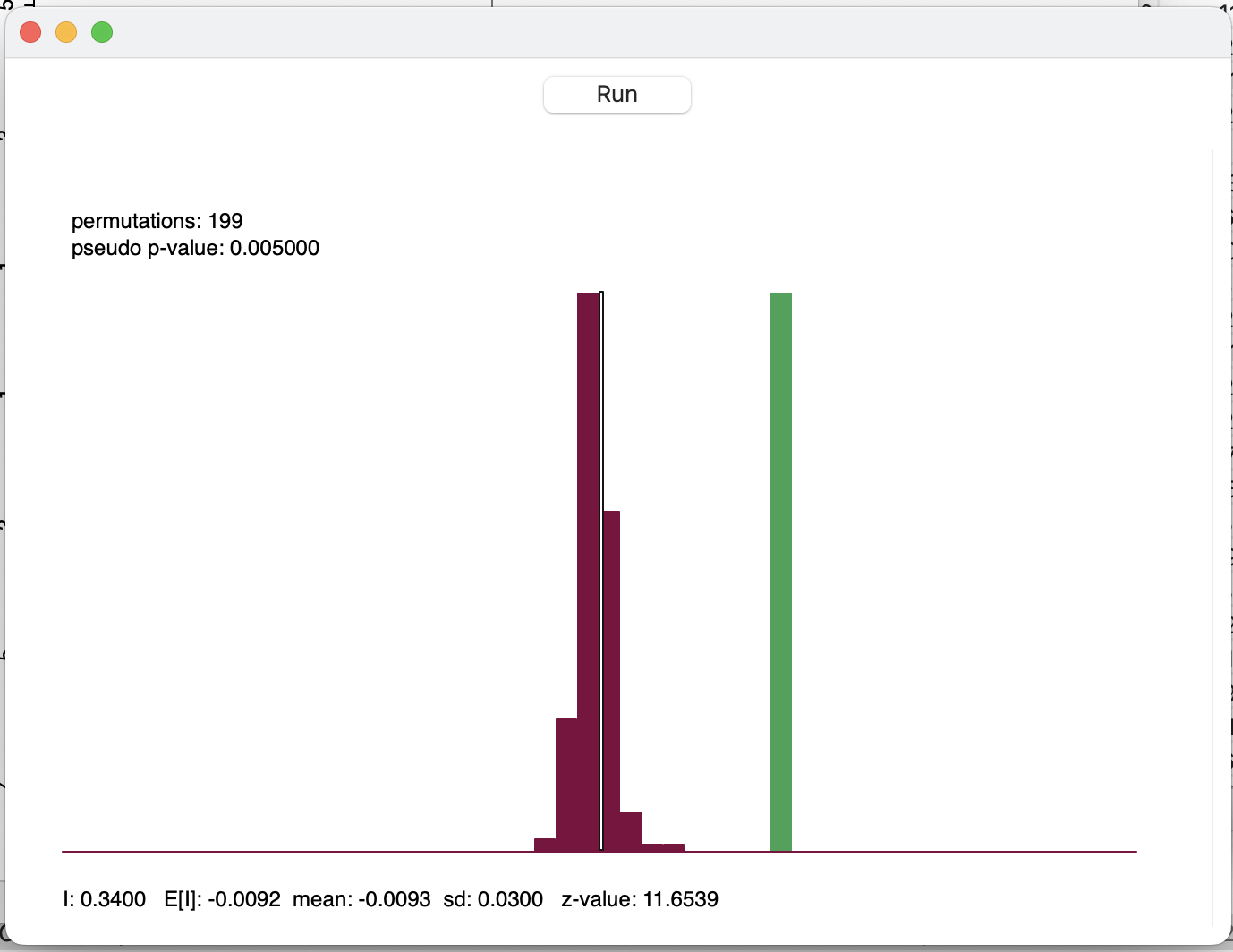
В представленном примере фактическое значение не попадает в график распределения, полученный случайными перестановками, что говорит о статистической значимости полученного индекса. То есть для рассматриваемой величины может быть отвергнута нулевая гипотеза о пространственной случайности.
Попробуйте протестировать на пространственную автокорреляцию несколько разных переменных с разными матрицами весов.
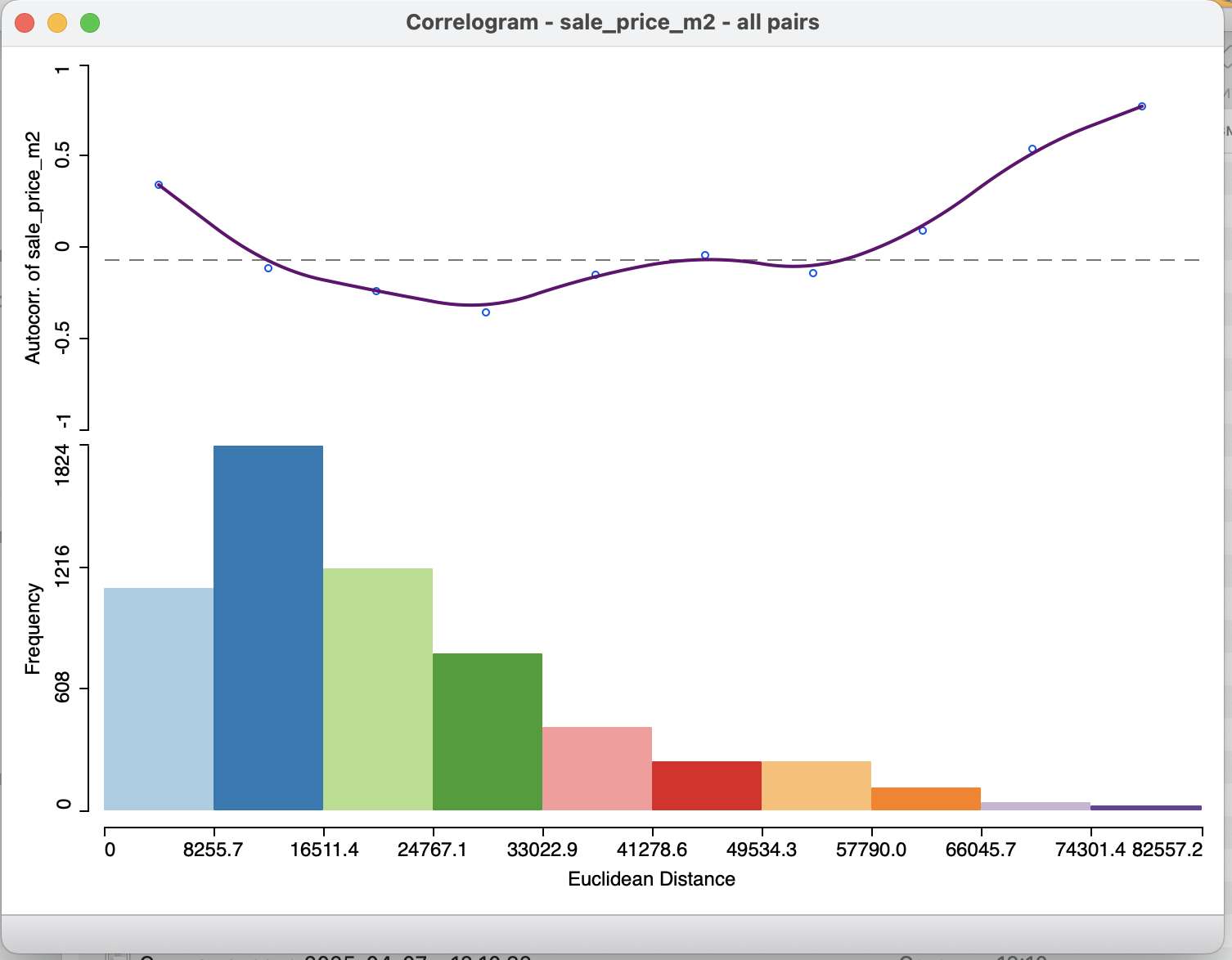
Кроме того с использованием инструмента Spatial correlogram вы можете протестировать коэффициент пространственной автокорреляции на разных расстояниях.
Этот график показывает зависимость коэффициента корреляции в зависимости от расстояния. Таким образом можно отследить изменение пространственного процесса в разных масштабах.
4 Локальная пространственная автокорреляция
Если глобальная пространственная автокорреляция дает общую оценку, то локальная пространственная автокорреляция позволяет выявить паттерны распределения величины и найти кластеры.
Следует понимать, что здесь речь идет несколько об иных кластерах, чем мы говорили в теме “Анализ точечных паттернов”. Если в той теме кластеры - это просто близкие объекты (если говорить о чисто пространственной кластеризации) или объекты с похожими характеристиками, то здесь кластеры - это группы похожих объектов значительно отличающихся от своего окружения.
В программе реализовано несколько различных индексов, но мы с вами будем использовать только локальную вариацию индекса Морана.
Расчет индексов локальной пространственной автокорреляции осуществляется либо инструментом Cluster maps ![]() , либо инструментом из строки меню:
, либо инструментом из строки меню:
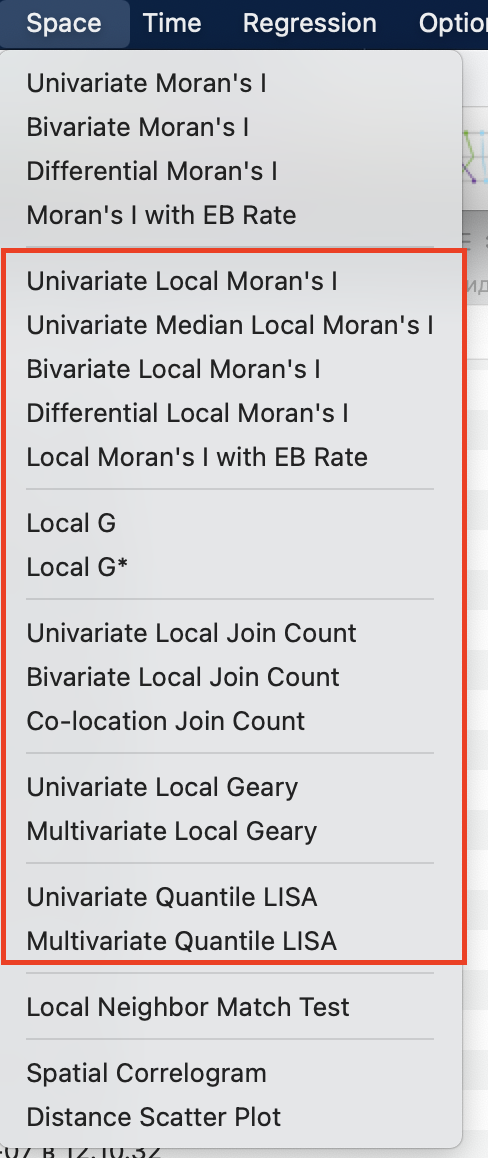
При использовании инструмента из панели инструментов меню будет немного отличаться, но будет содержать все доступные методы для тестирования на локальную пространственную автокорреляцию.
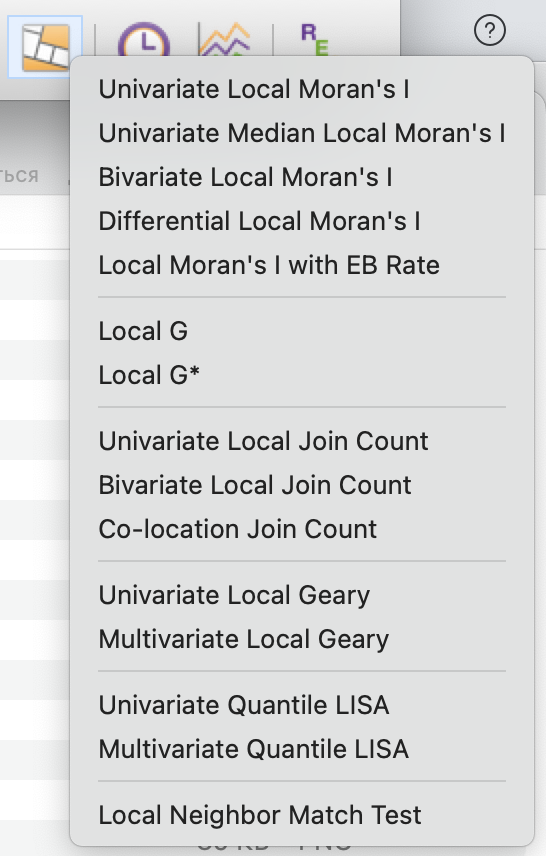
Вариации индекса Морана здесь такие же, как и для глобального индекса.
Точно также, как и при вычислении глобального индекса необходимо выбрать интересующую вас переменную и матрицу весов.
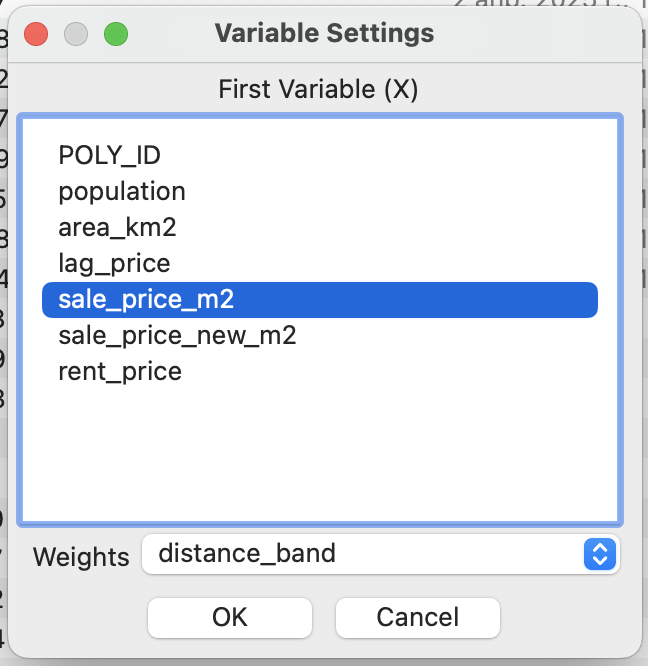
После выбора вам предлагается несколько вариантов вывода результата расчета локальной пространственной автокорреляции:
Significance map - карта статистической значимости полученных значений локальных индексов;
Cluster map - карта выявленных кластеров;
Moran scatter plot - график Морана.
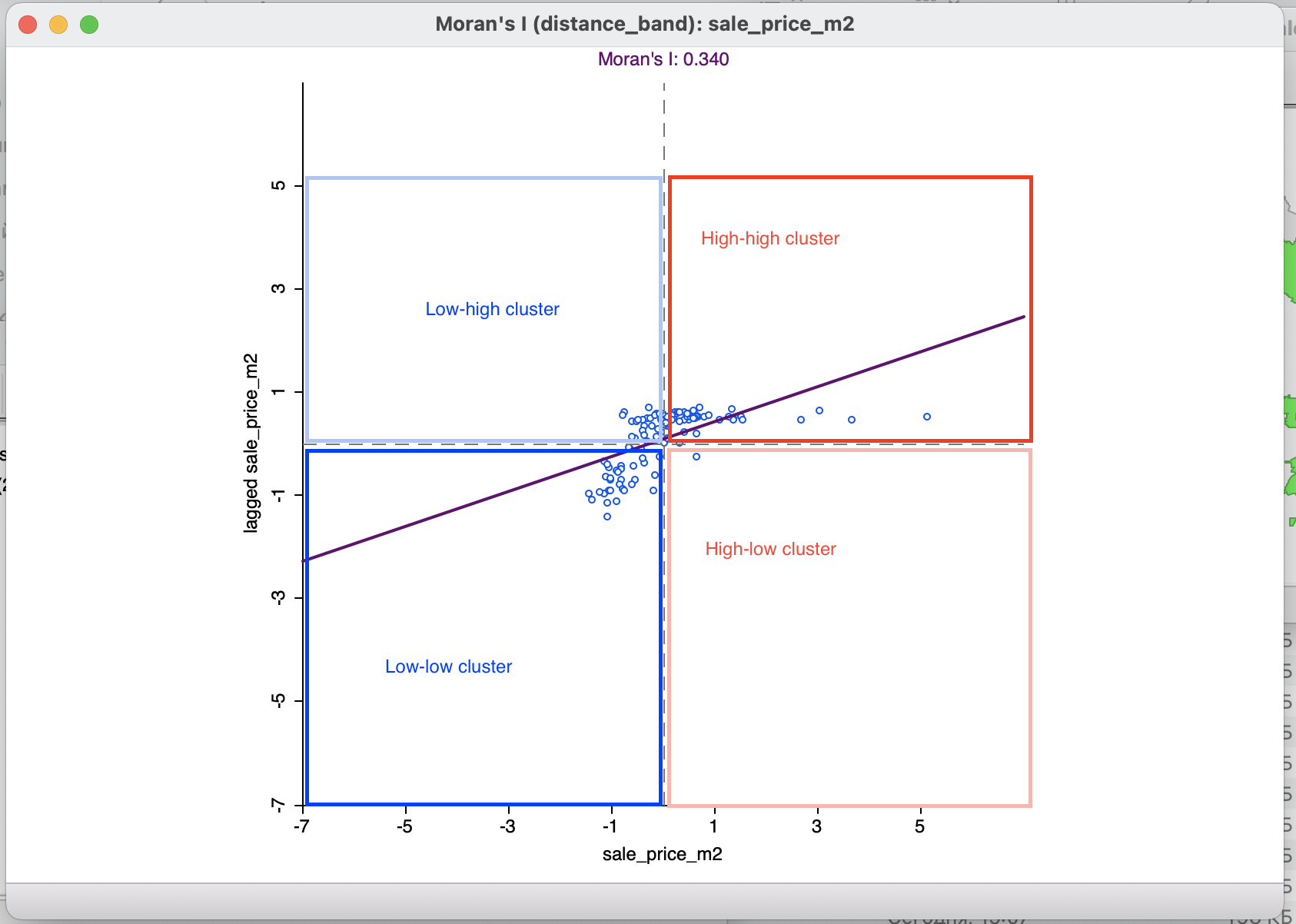
График Морана здесь строится аналогично предыдущему разделу, но может уже более подробно интерпретироваться с точки зрения принадлежности объектов к тем или иным группам:
квадрант с высоким значением переменной и высоким значением пространственного лага (High-High -квадрант);
квадрант с низким значением переменной и низким значением пространственного лага (Low-low-квадрант);
квадрант с высоким значением переменной и низким значением пространственного лага (High-Low-квадрант);
квадрант с низким значением переменной и высоким значением пространственного лага (Low-High-квадрант).
Полученная карта значимости показывает статистическую значимость рассчитанных коэффициентов локальной пространственной автокорреляции.
В легенде указан уровень значимости для тех объектов, для которых коэффициенты являются статистически значимыми.
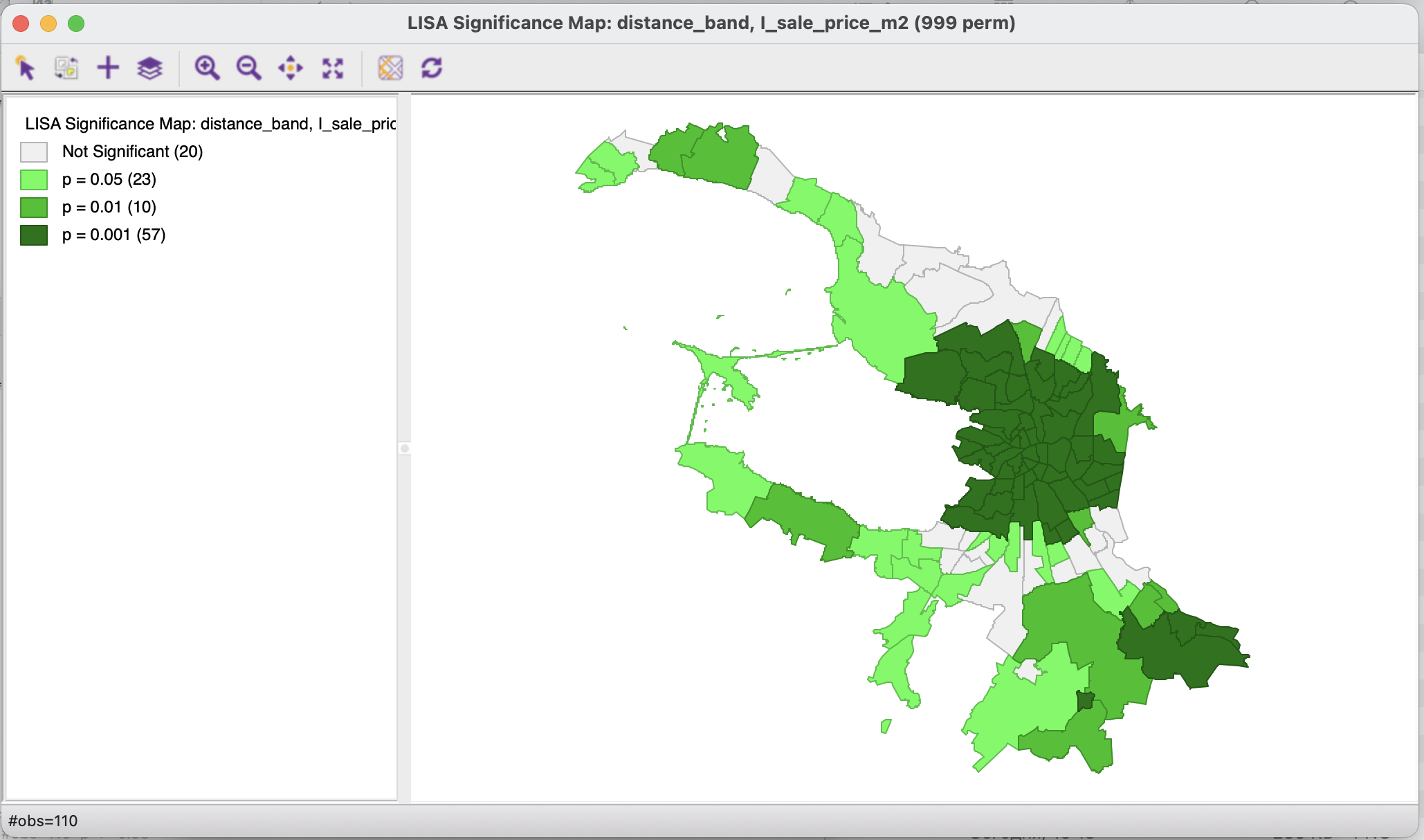
На карте кластеров показаны выявленные кластеры. Фактически здесь все объекты раскрашены цветом в зависимости от того, в какой квадрант из перечисленных выше они попадают, за исключением тех из них, для которых значение локального индекса не является статистически значимым.
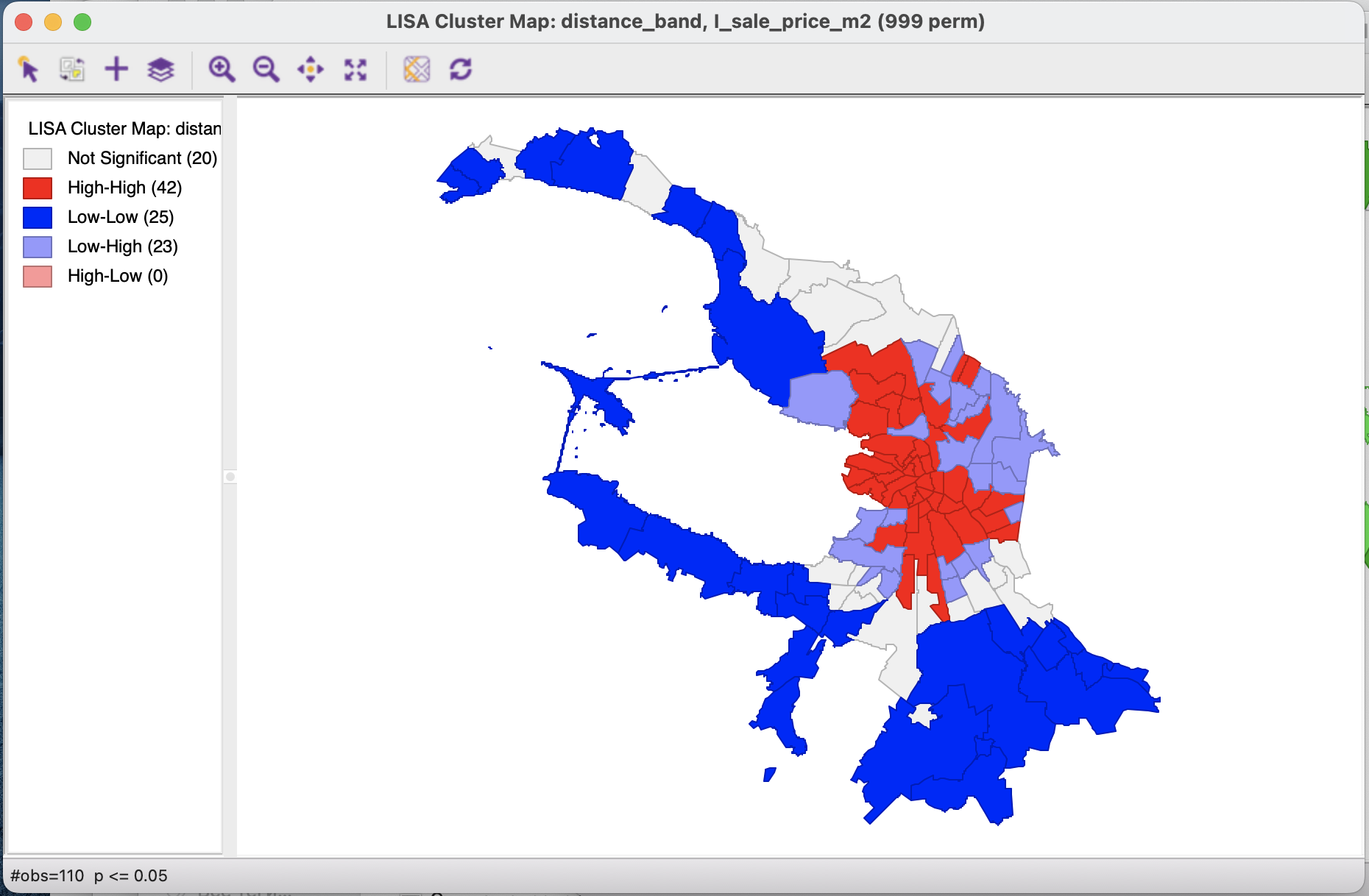
Здесь как и для глобальной пространственной автокорреляции будет большую роль играть матрица пространственных весов.
Попробуйте рассчитать индексы локальной пространственной автокорреляции для различных матриц пространственных весов и сравнить их между собой, а также попробовать проинтерпретировать ваши результаты.