Пространственные веса
1 Программа GeoDa
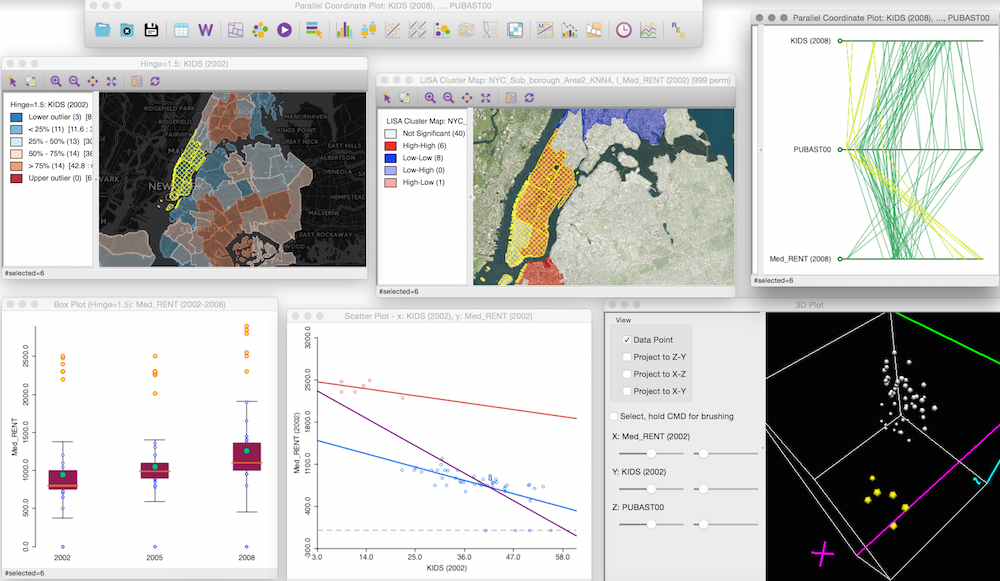
GeoDa - это бесплатный программный инструмент с открытым исходным кодом, который служит для ознакомления с пространственной наукой о данных. Он разработан для того, чтобы способствовать получению новых выводов на основе анализа данных путем изучения и моделирования пространственных моделей.
Сайт программы: https://geodacenter.github.io/ (на нем же можно скачать файл установки программы).
Ознакомиться с документацией можно по ссылке.
Основной интерфейс программы состоит из панели инструментов и строки меню.

GeoDa поддерживает основные векторные форматы пространственных данных, а также подключение к базам данных и использование векторных данных с веб-ресурсов в формате .geojson и WFS.
При запуске программы у вас появится окно открытия источника данных.
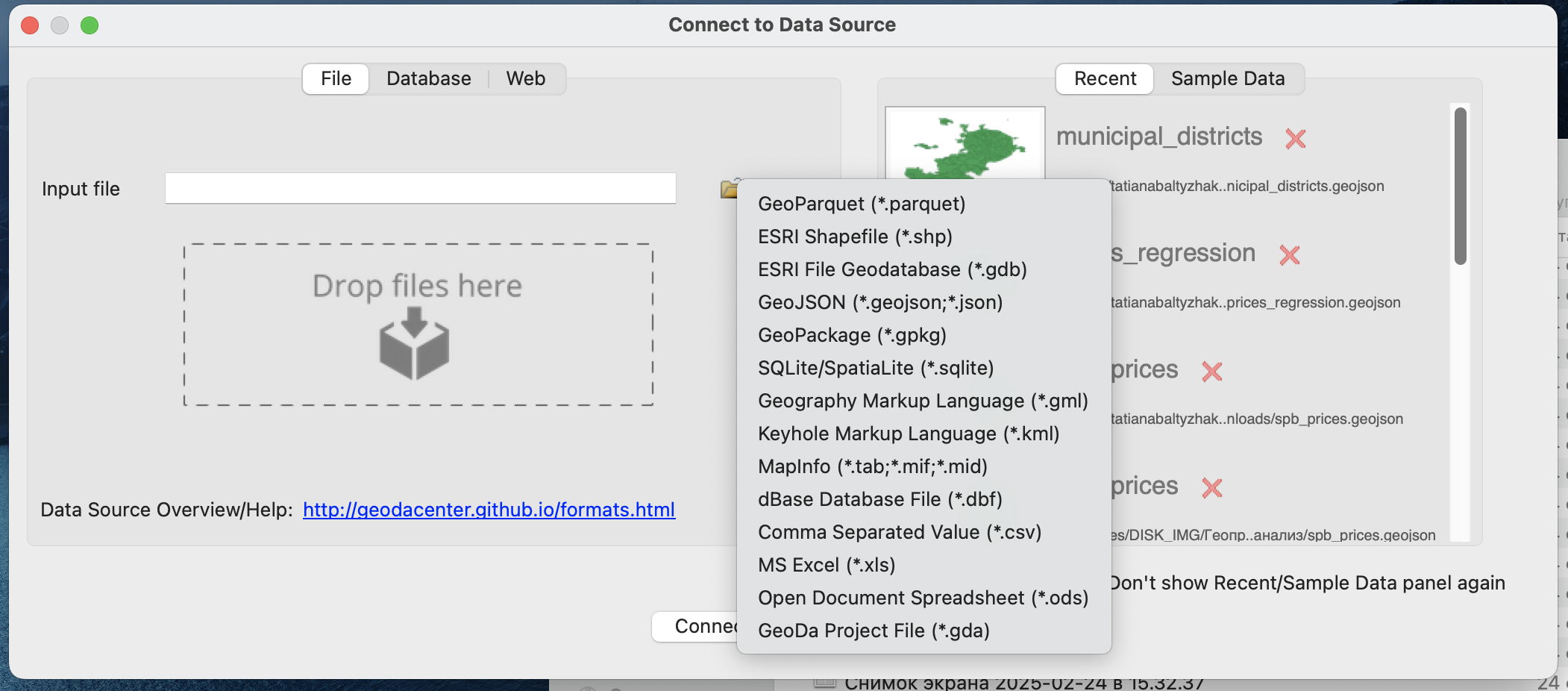
В том случае, если это окно не открылось, необходимый вам файл можно открыть по клику на значок ![]() .
.
2 Исходные данные
В качестве исходных данных будет использоваться набор данных о стоимости недвижимости в Санкт-Петербурге, который можно скачать по ссылке.
Относитесь к этим данным как к синтетическим, так как их источник ненадежен.
3 Общие инструменты работы с данными
После того, как вы открыли файл с исходными данными, у вас появится окно карты.
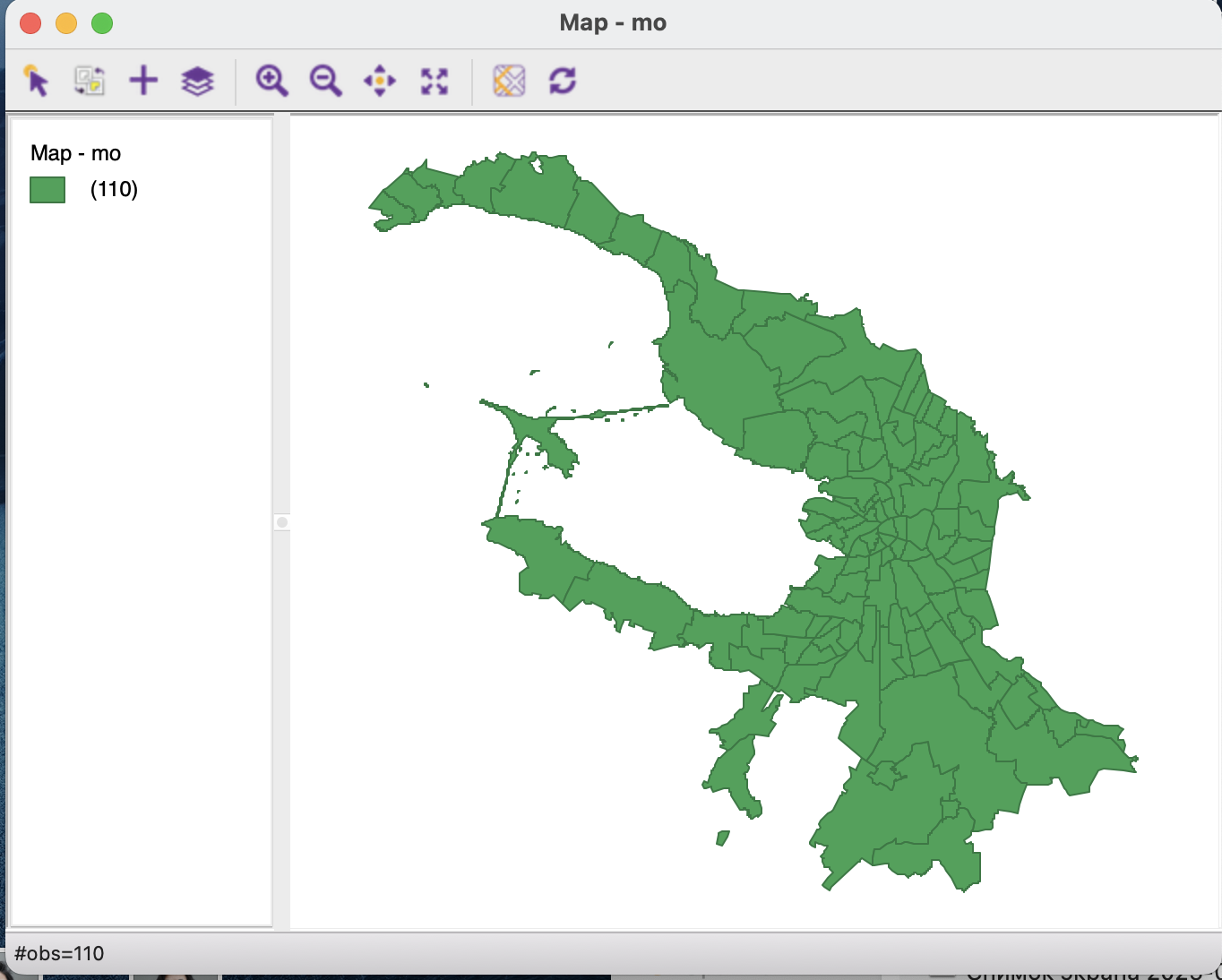
В этой карте как и в прочих геоинформационных системах вы можете добавить подложку для контекста с использованием иконки ![]() .
.
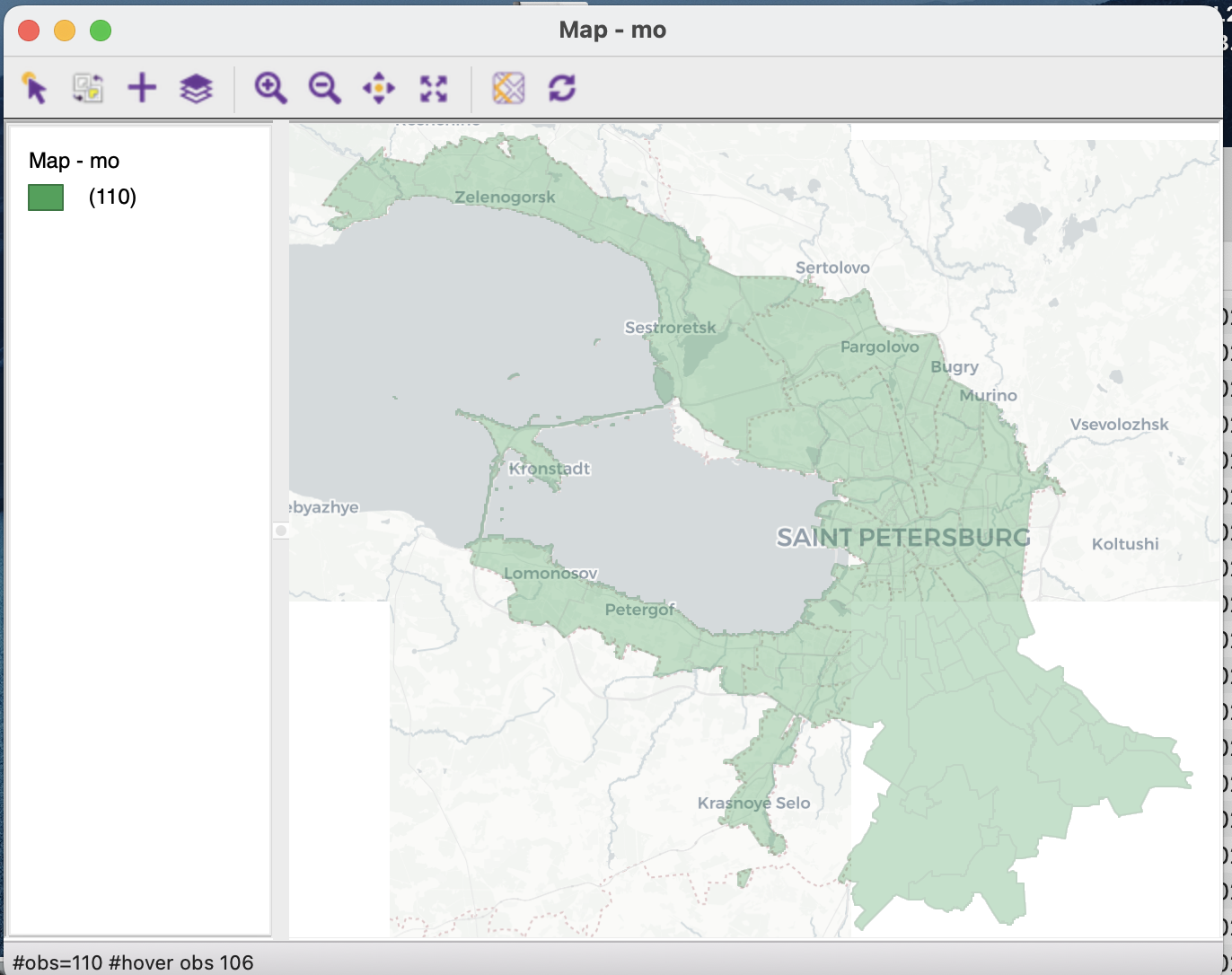
Кроме открытия слоя с имеющейся геометрией программа имеет функции по созданию геометрии точечного слоя из таблицы или создания сетки, а также пространственного объединения слоев (Spatial join) и слияния объектов (Dissolve).
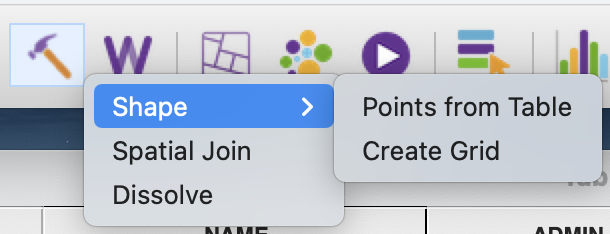
Пространственное объединение позволяет объединять объекты из разных слоев, а слияние - объекты одного слоя по значению атрибута (например, мы могли бы так объединить муниципальные образования в районы).
Настройка карты для визуализации показателя может быть осуществлена двумя способами:
- через строку меню;
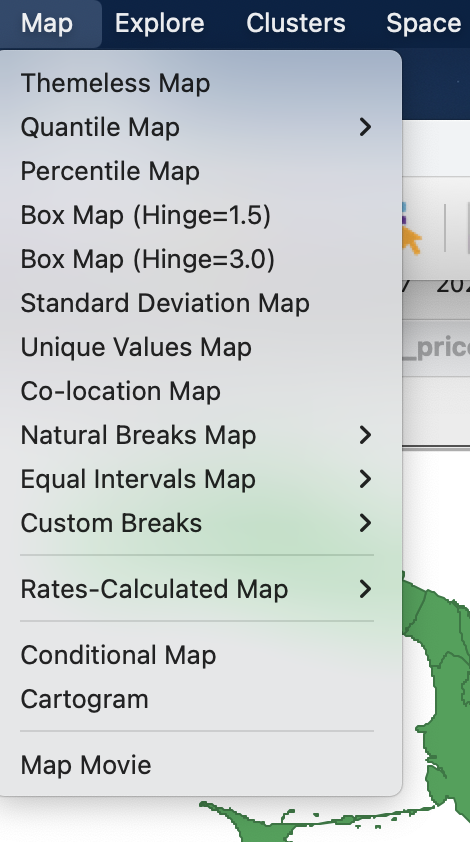
- правым кликом на карте
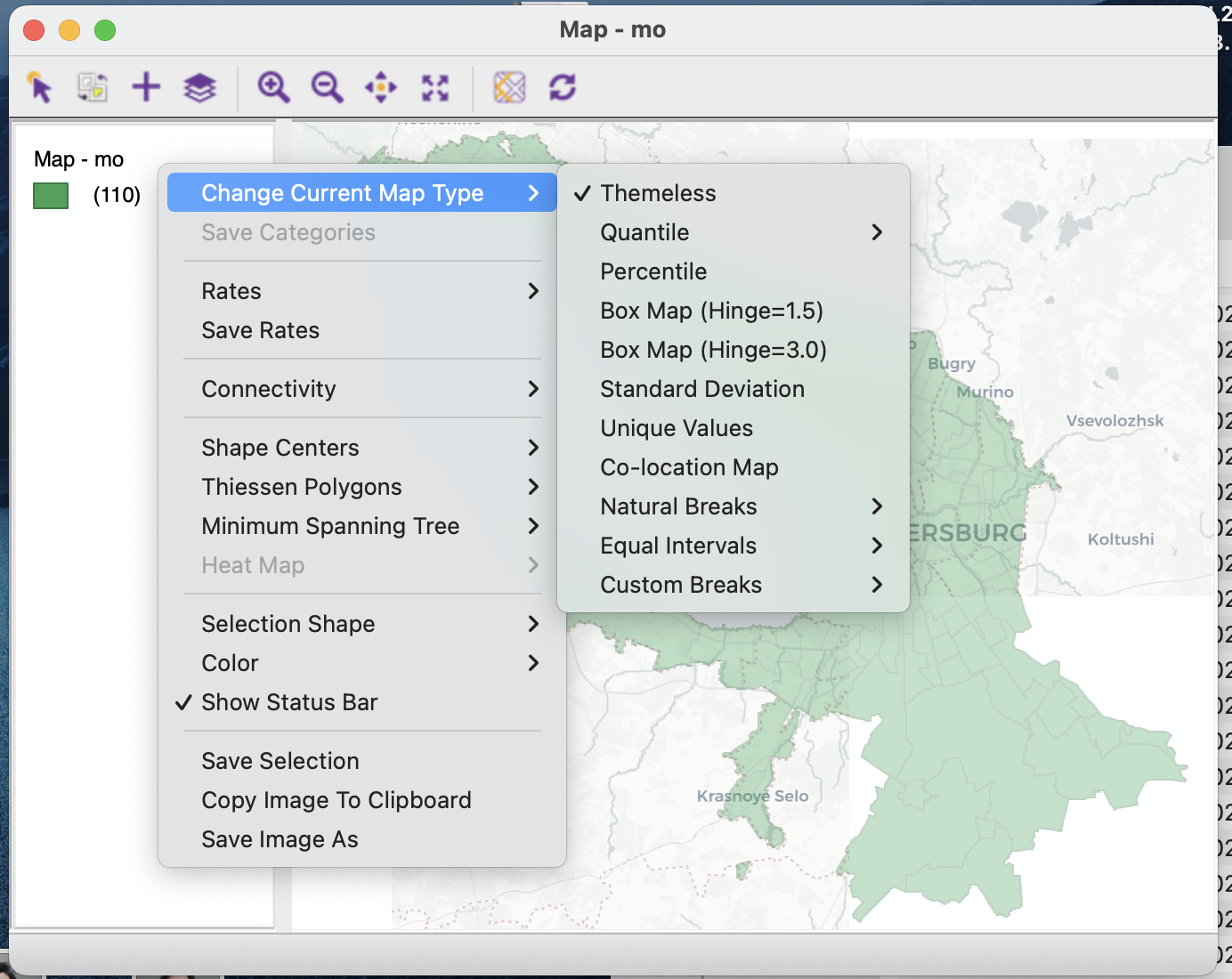
Настройка здесь может быть осуществлена на основе стилей/тем по умолчанию, либо создана в виде кастомных интервалов.
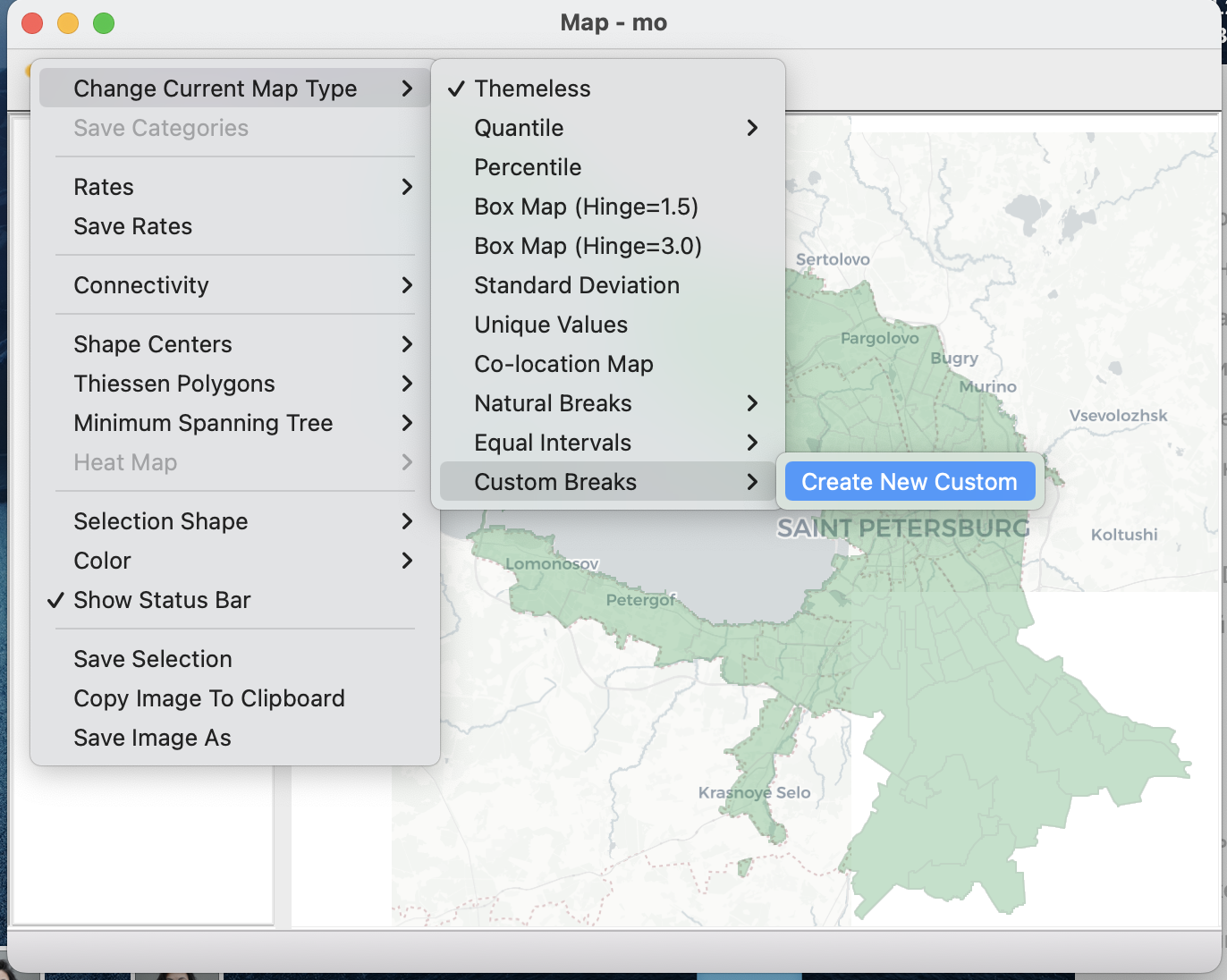
На самом деле любой стиль по умолчанию можно подредактировать при необходимости и получить свой собственный стиль. Для этого нужно просто открыть редактор категорий ![]() .
.
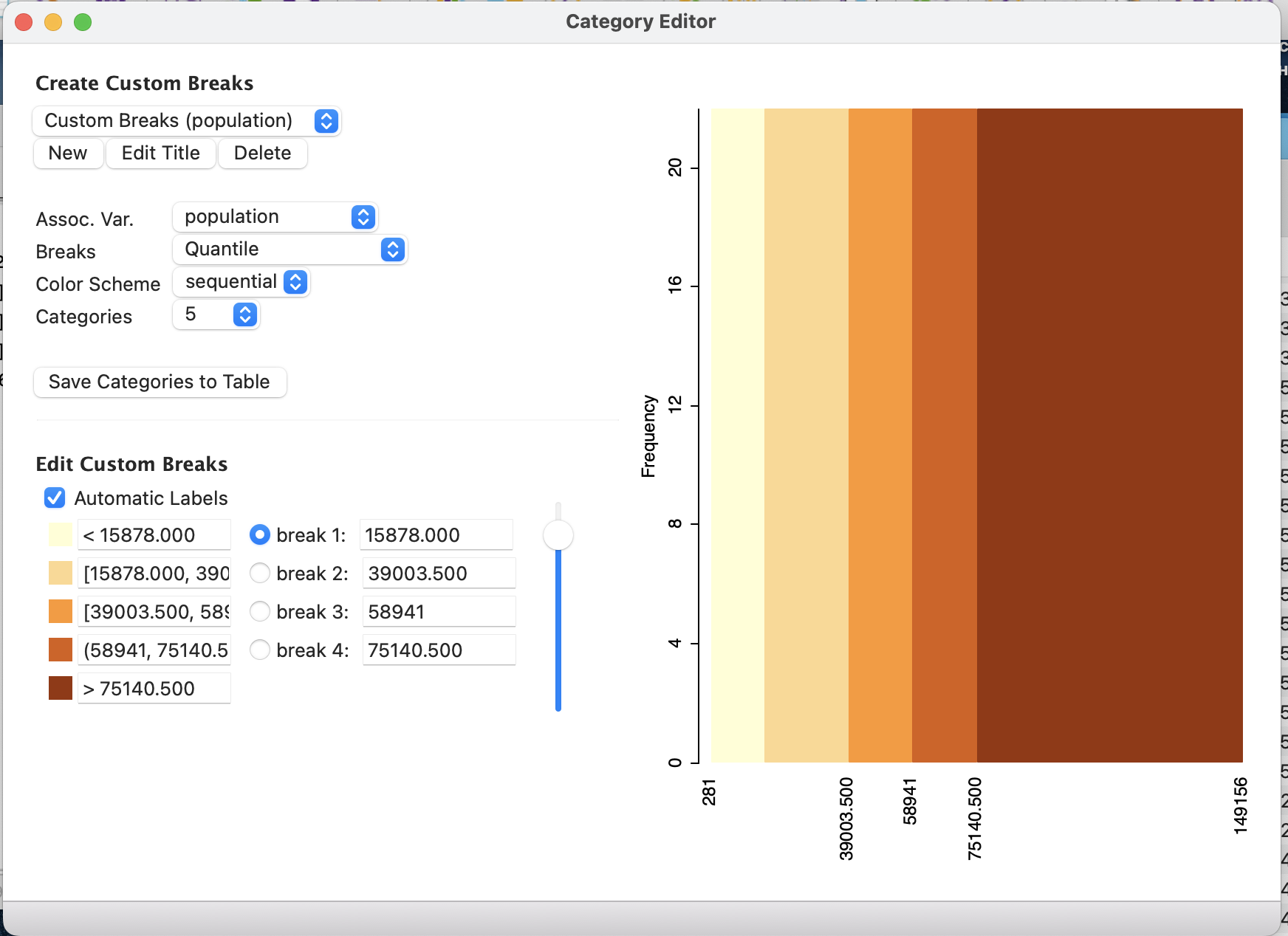
При необходимости сохранения интервалов, вы можете это сделать, просто кликнув правой кнопкой мыши и выбрав Save rates. Тогда номера интервалов будут сохранены в атрибутивную таблицу.
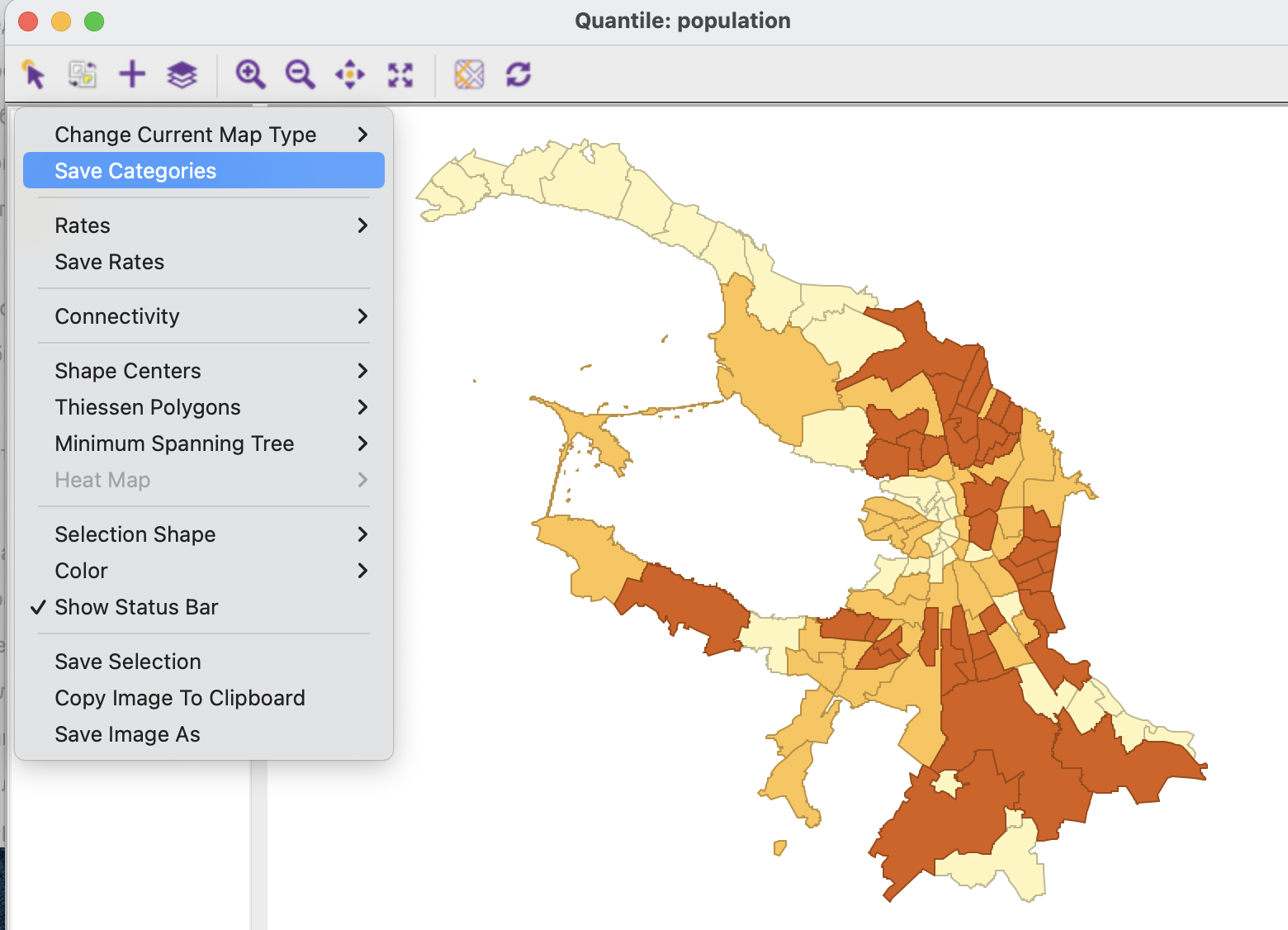
Кроме обычной фоновой картограммы, также есть опция создания картограммы Дорлинга  , в которой все объекты будут заменены на круги различного диаметра в зависимости от значения показателя.
, в которой все объекты будут заменены на круги различного диаметра в зависимости от значения показателя.
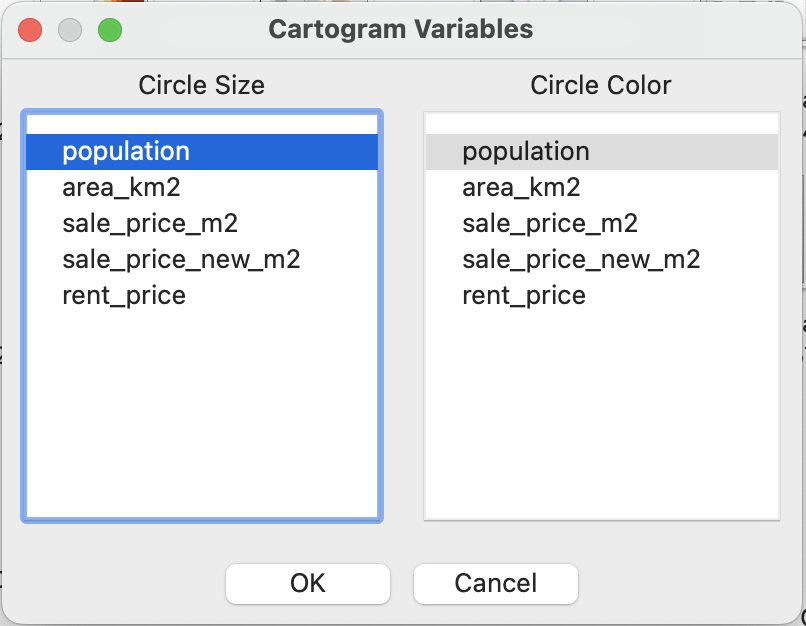
Причем отдельно здесь можно указать, что будет обозначать цвет символа, а что - его размер.
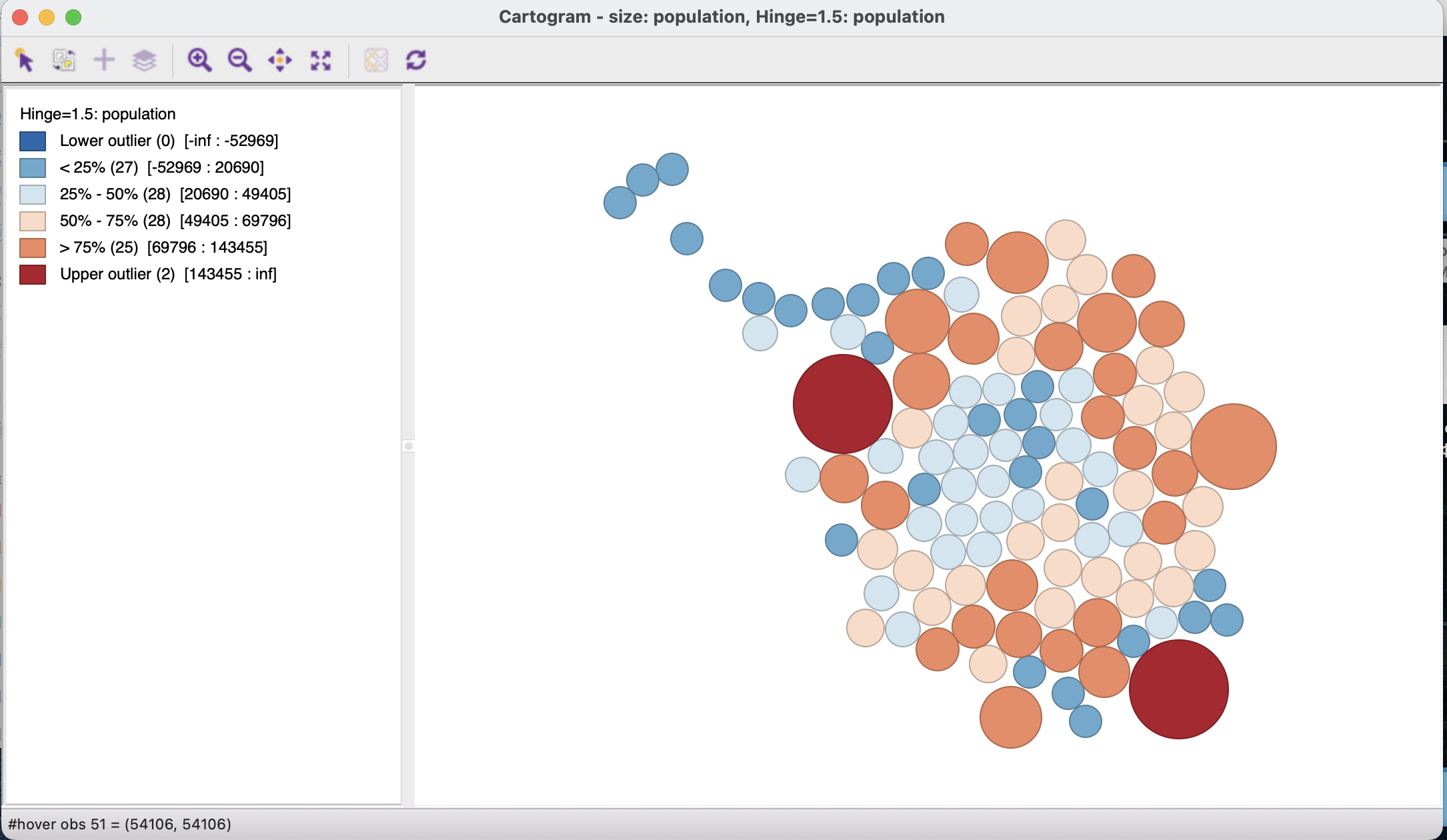
Полученная картограмма также может быть отдельно донастроена по цветовой палитре.
Атрибутивную таблицу можно открыть в отдельном окне по клику на иконку ![]() .
.
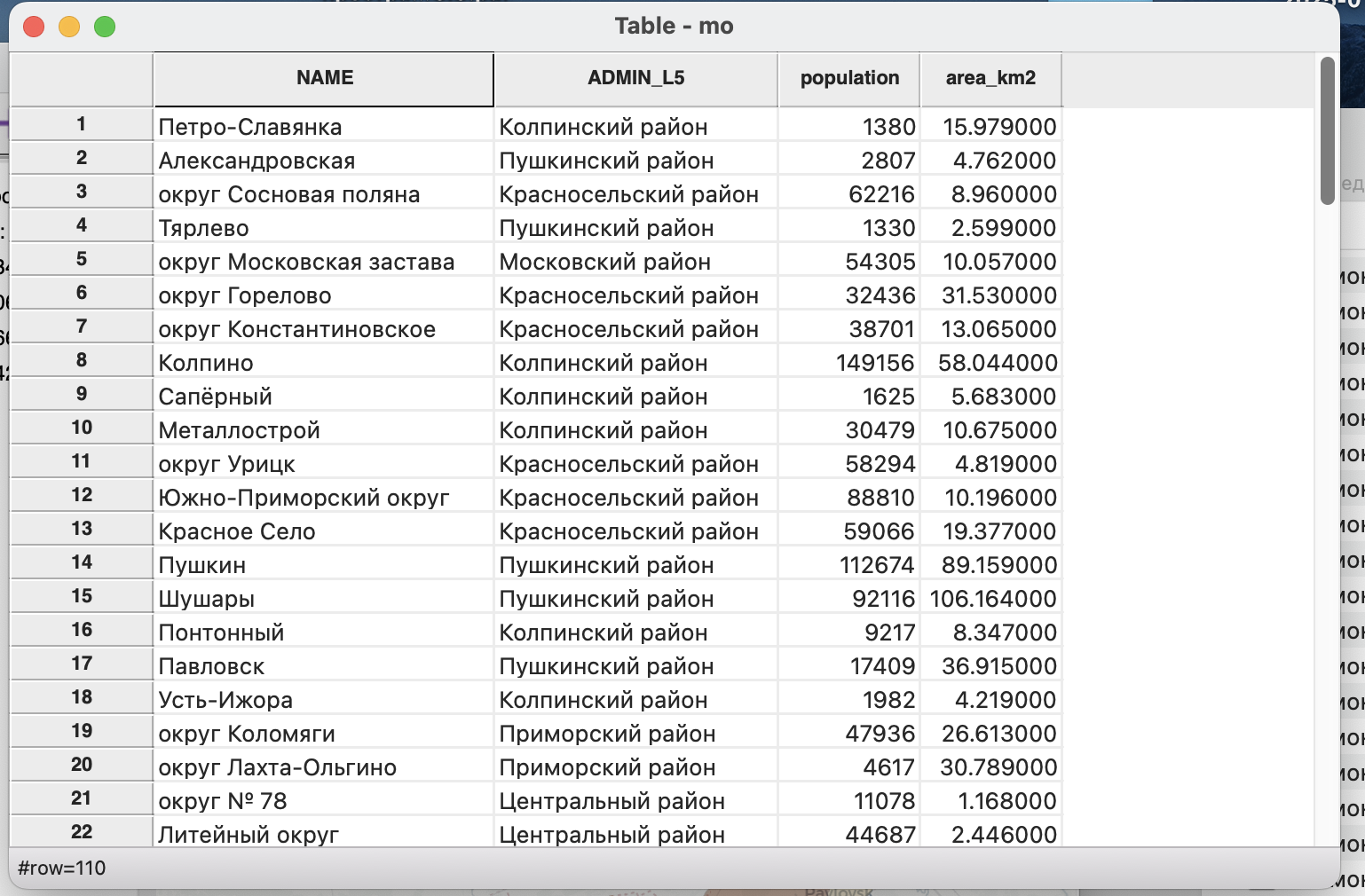
В строке меню есть отдельный пункт Table, который содержит в себе инструменты для работы с таблицами.
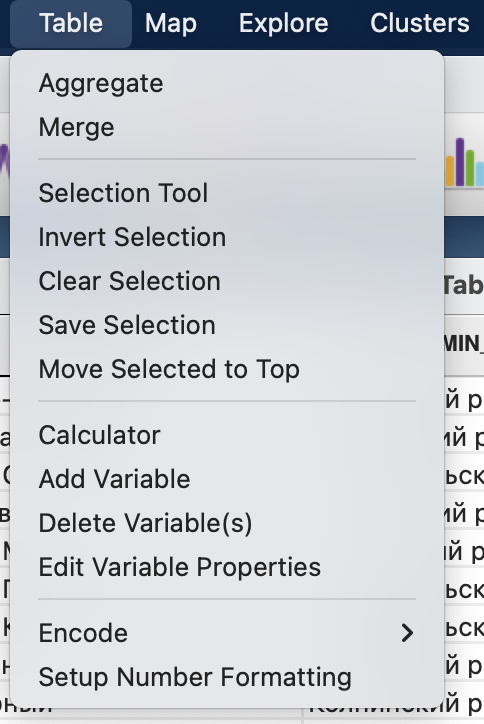
При необходимости вы можете добавлять или удалять атрибуты, а также редактировать типы данных в столбцах, если они были определены при открытии неправильно.
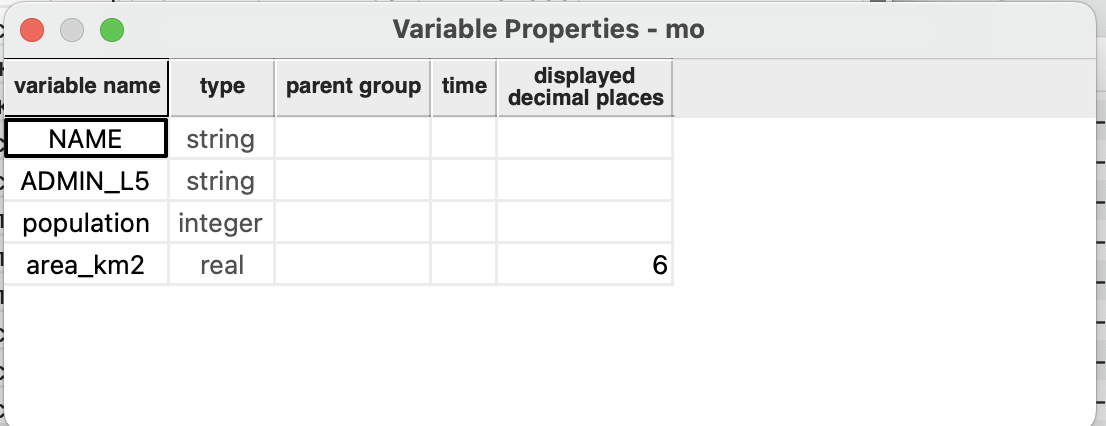
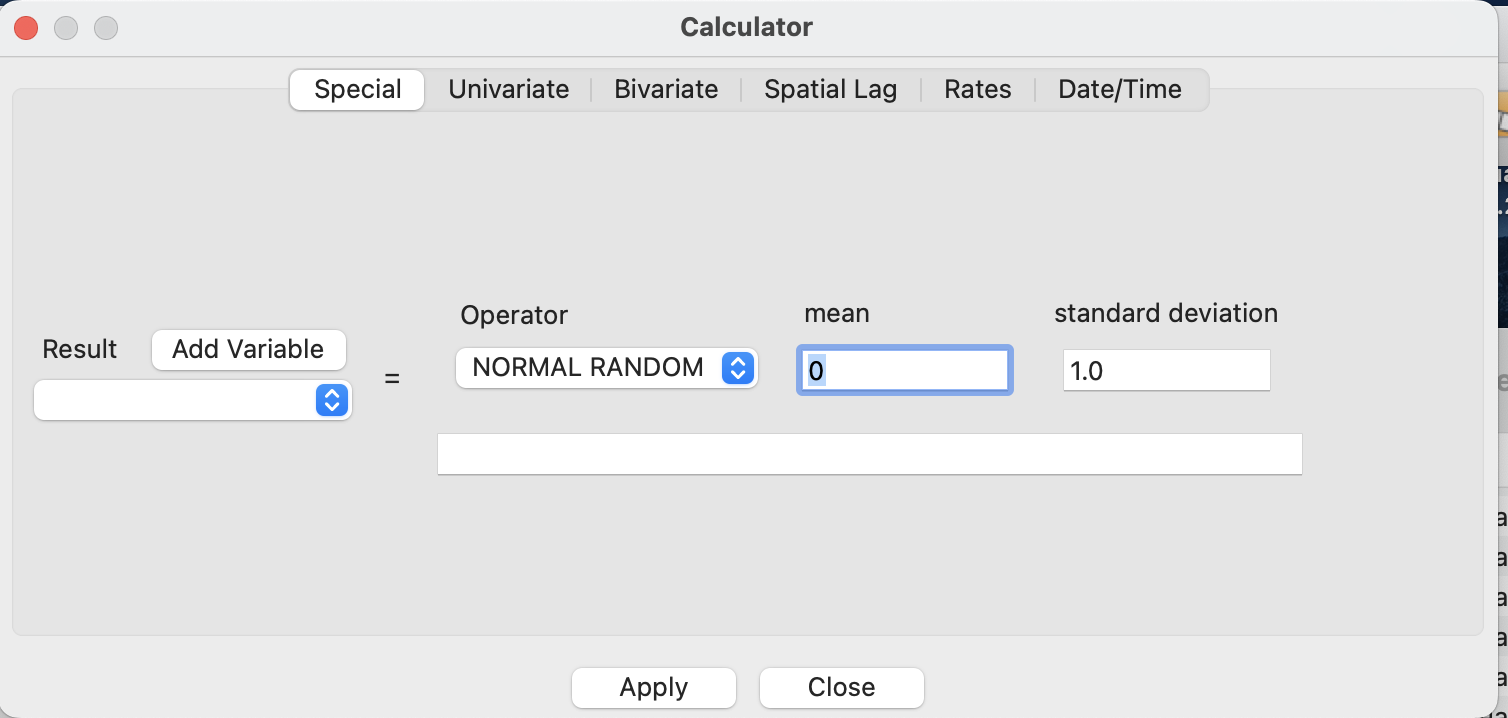
Для атрибутивной таблицы есть калькулятор полей, позволяющий осуществлять расчеты.
Также в программе есть довольно большой выбор инструментов для исследовательского анализа данных, представленных в основной панели инструментов.

4 Расчет пространственных весов
Для создания матрицы пространственных весов необходимо воспользоваться менеджером весов ![]() , также его можно открыть из строки меню.
, также его можно открыть из строки меню.
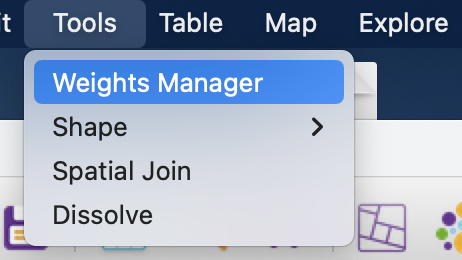
В открывшемся окне менеджера весов вы увидите опции для создания новых и загрузки уже рассчитанных матриц пространственных весов.
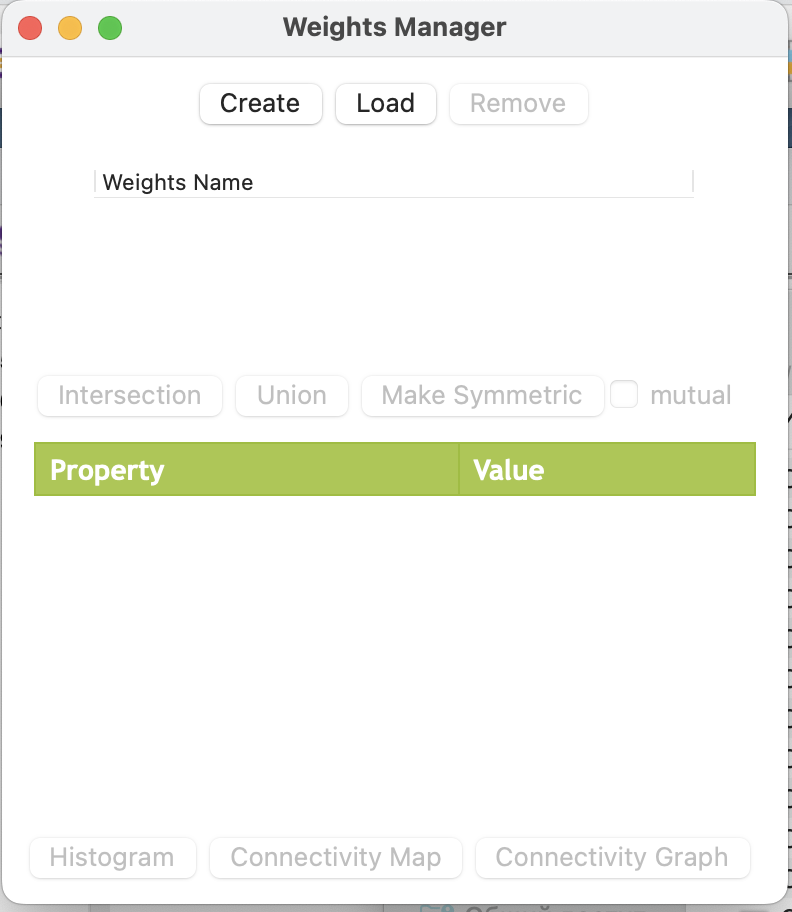
После начала создания матрицы пространственных весов вы увидите окно, в котором можно выбрать тип рассчитаваемого веса.
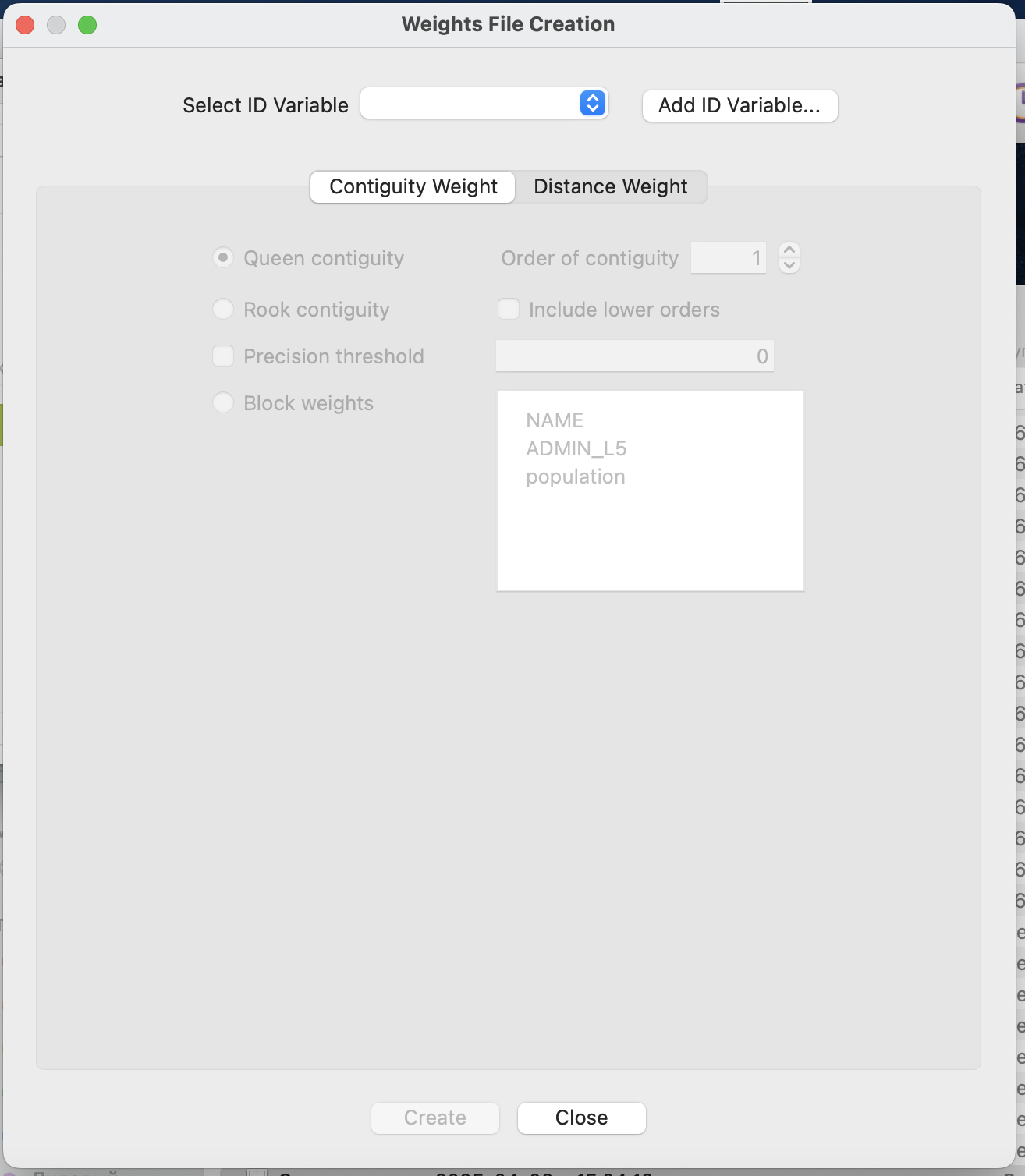
Очень важно, чтобы при создании матрицы весов у каждого объекта в наборе данных был уникальный идентификатор - порядковый номер, если такого идентификатора нет, то его можно просто создать Add ID variable.
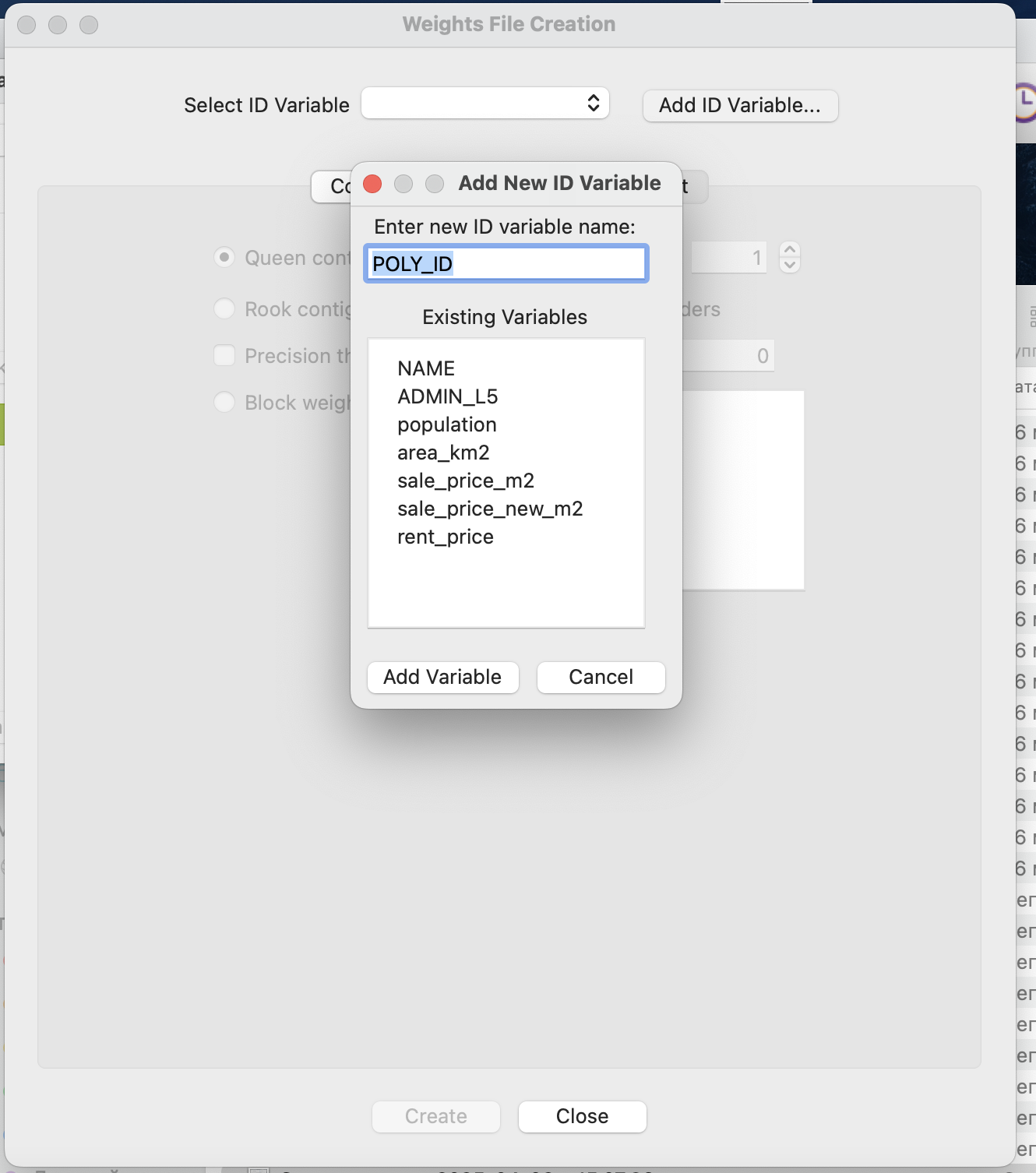
Все матрицы весов сохраняются во внутреннем формате программы: два разных формата - один для матриц по смежности, второй - для матриц на основе расстояния. При необходимости они могут быть открыты просто в текстовом редакторе.
4.1 Расчет весов по смежности
4.1.1 Принцип ферзя (королевы)
Для того, чтобы объекты считались соседями, достаточно, чтобы у них была хотя бы одна общая точка.
При создании весов по смежности достаточно выбрать используемый принцип смежности и порядок (мы везде по умолчанию используем только первый порядок соседства).
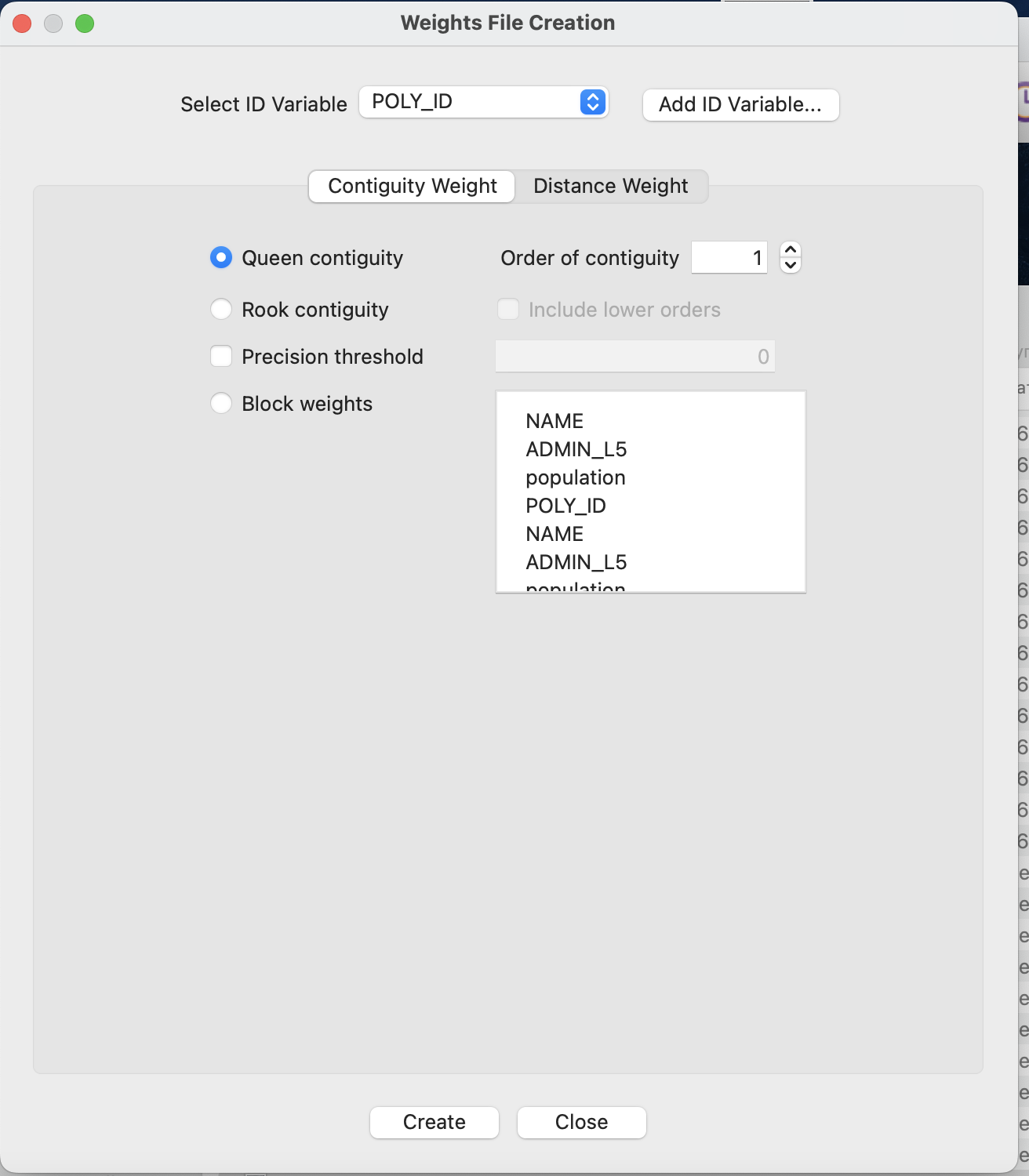
Параметр Precision threshold (порог точности) здесь нужен в том счучае, если вы сомневаетесь в качестве своих исходных данных и корректном примыкании пространственных объектов друг к другу, так как позволяет задать размер потенциального зазора или наложения.
После создания вам будет предложено сохранить матрицу весов в специализированном формате. Полученная матрица появится в менеджере весов.
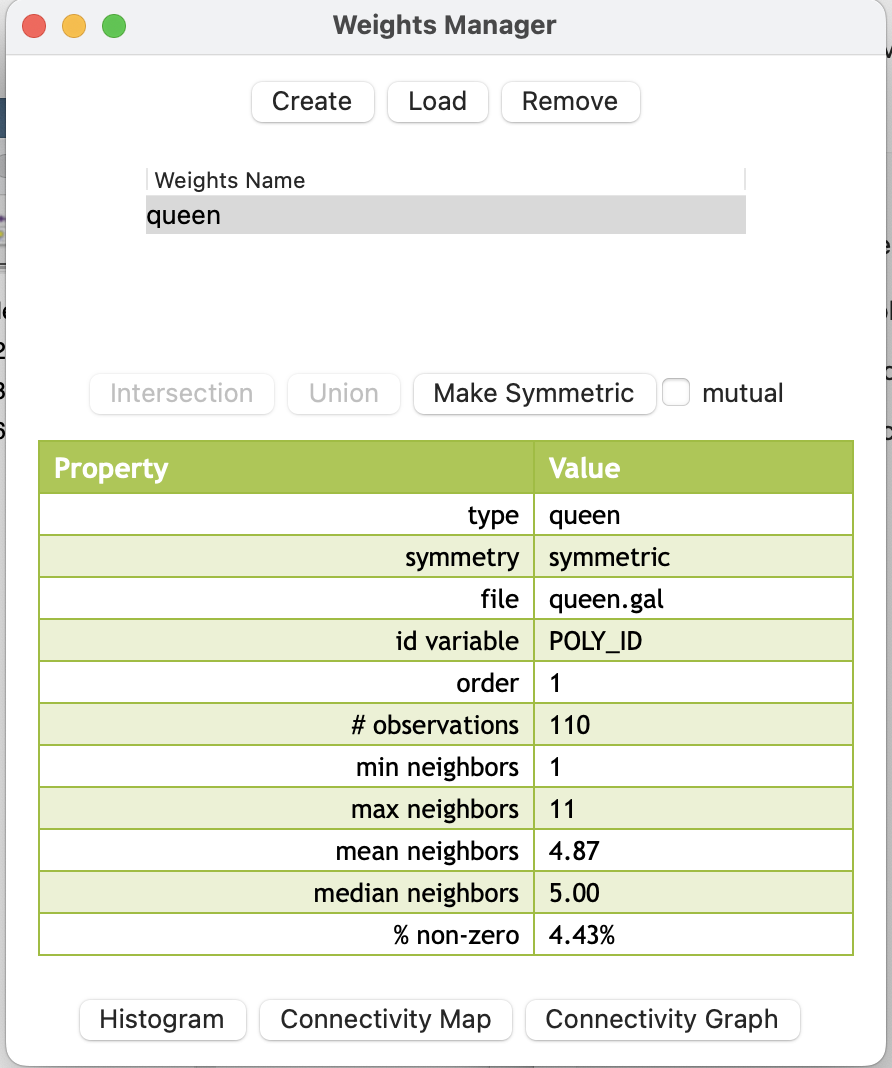
В менеджере весов вы можете ознакомиться с параметрами каждой матрицы:
ее тип;
симметричность;
название файла, в котором она сохранена;
атрибут с порядковым номером;
порядок соседства (для матриц по смежности);
количество наблюдений;
минимальное и максимальное число соседей внутри набора данных;
среднее и медианное число соседей;
процент ненулевых элементов матрицы.
Кроме того, вы можете изучить матрицу весов визуально с помощью гистограммы, карты или графа связности.
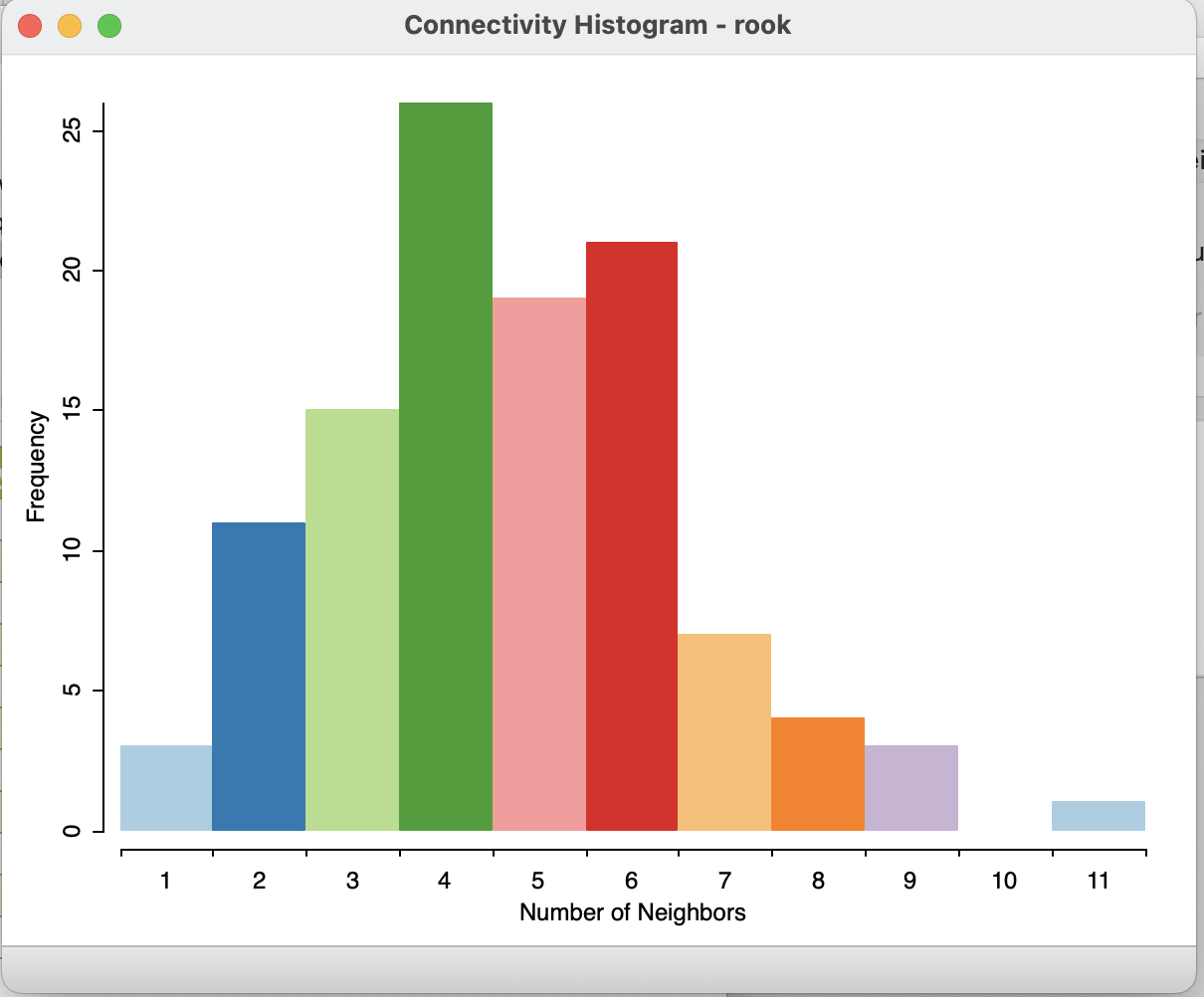
На гистограмме высота столбцов показывает количество объектов, имеющее определенное число соседей, которое показано по оси X.
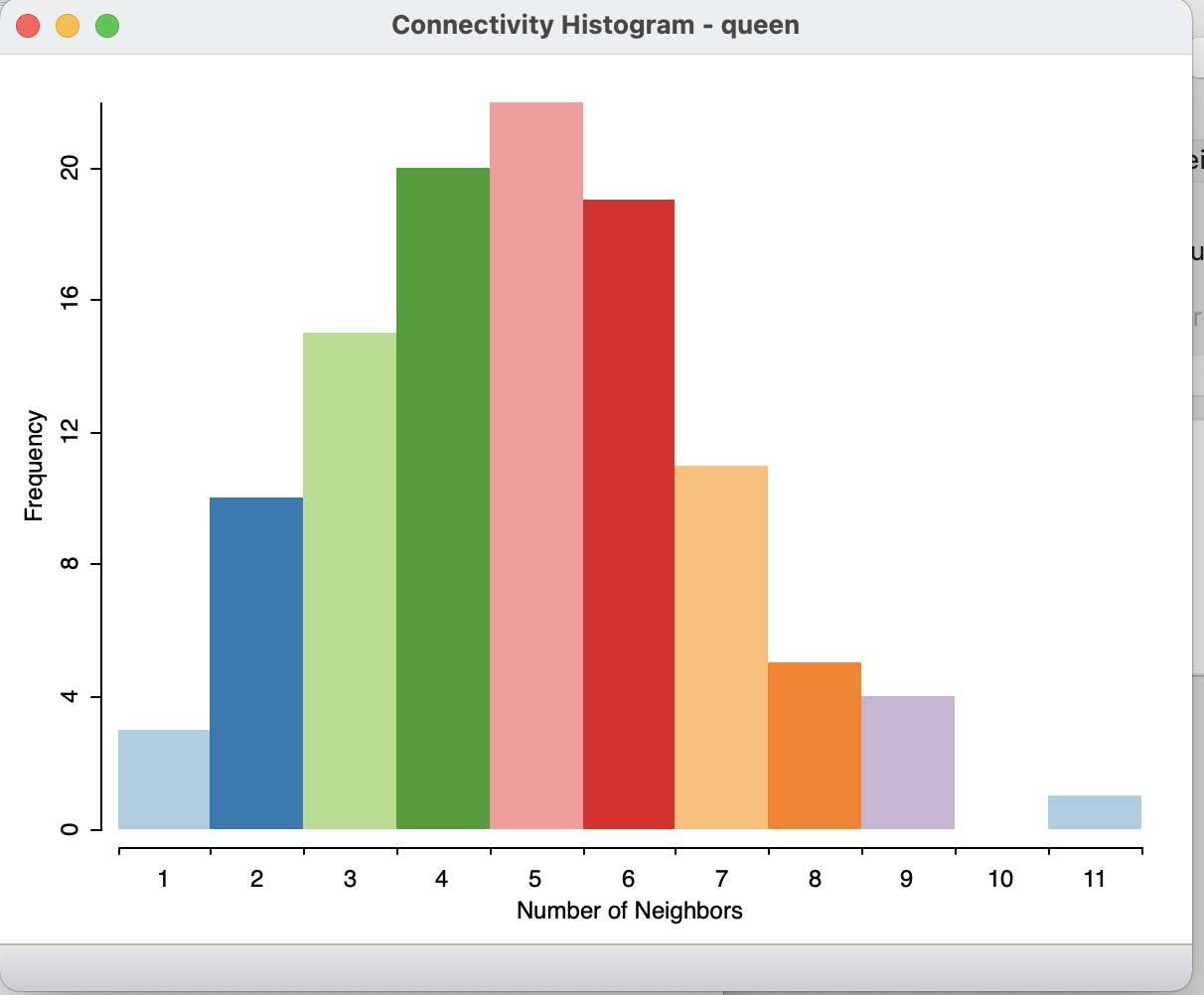
При выделении любого из столбиков вы сможете увидеть на карте, про какие именно объекты идет речь.
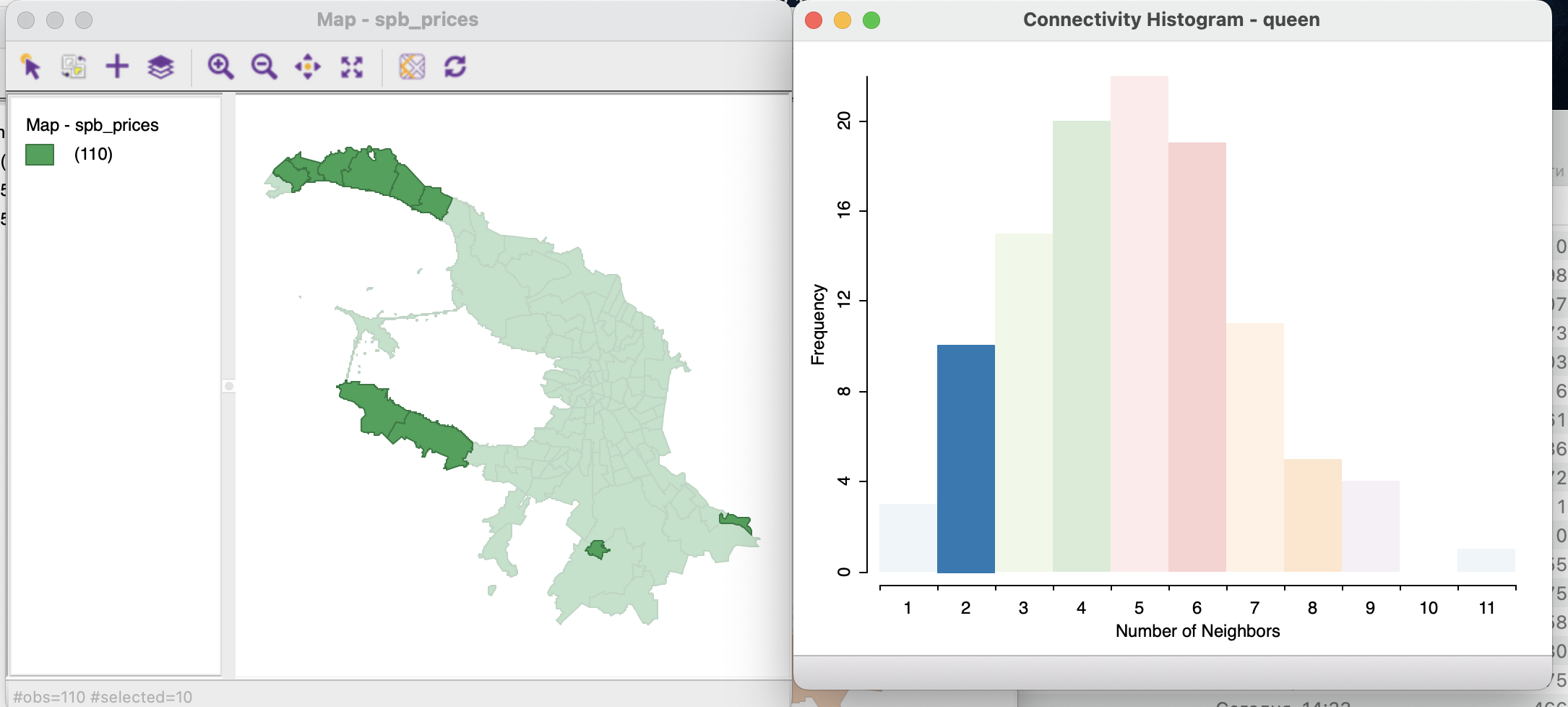
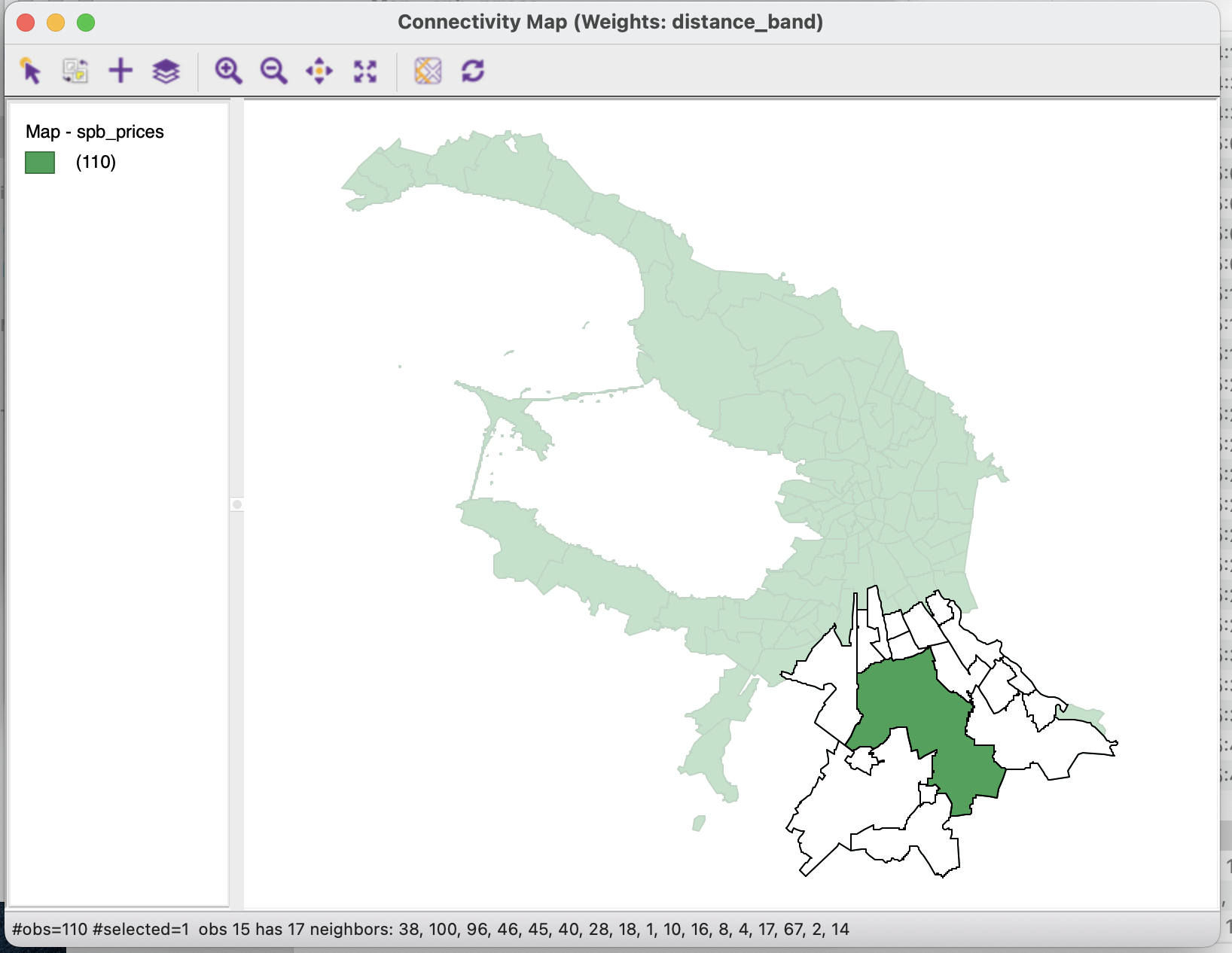
Карта связности показывает выделенный объект, на который наведен курсор (зеленым цветом) и его соседей в соответствии с матрицей весов.
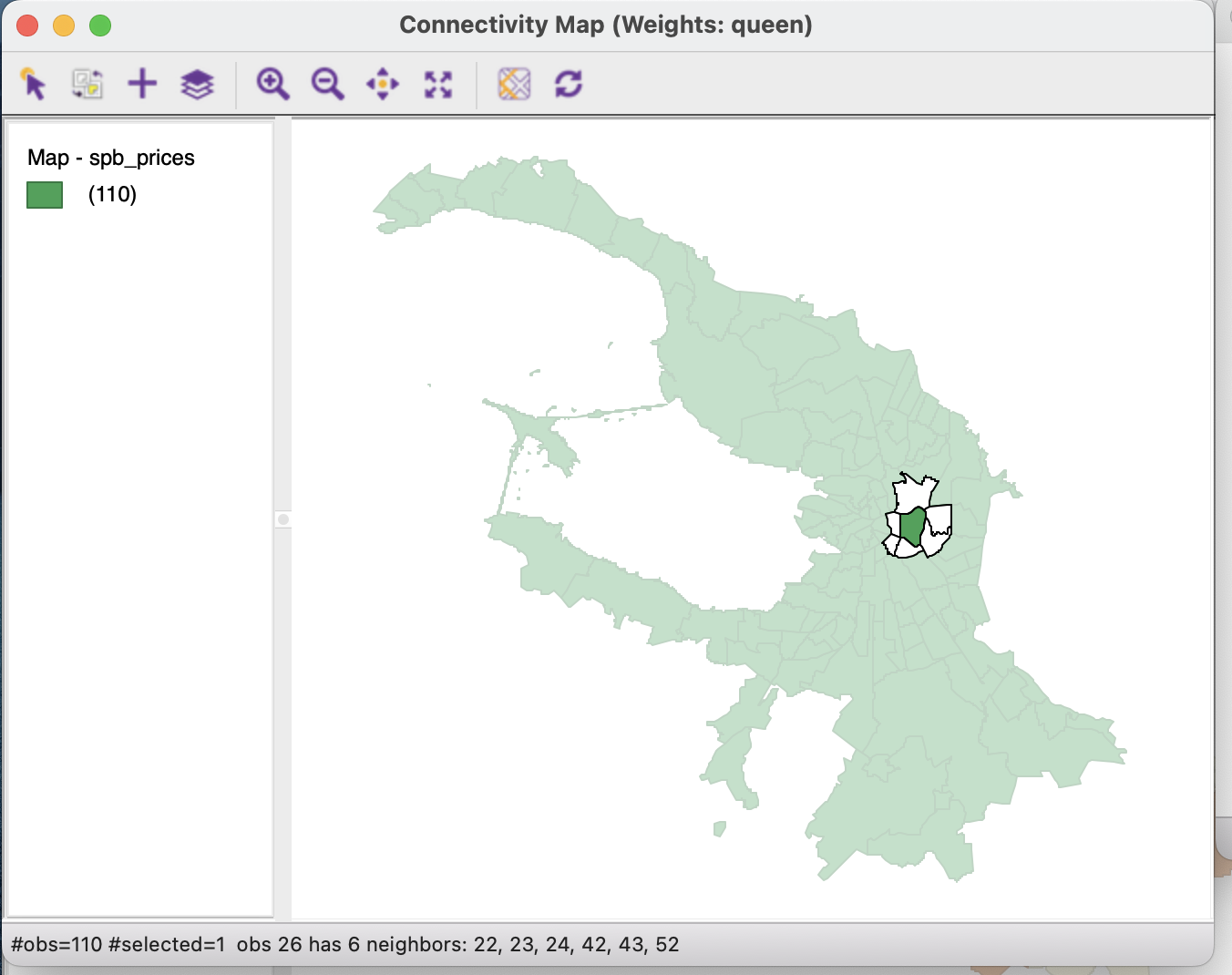
Граф связности же отображает топологические связи между объектами соседями.
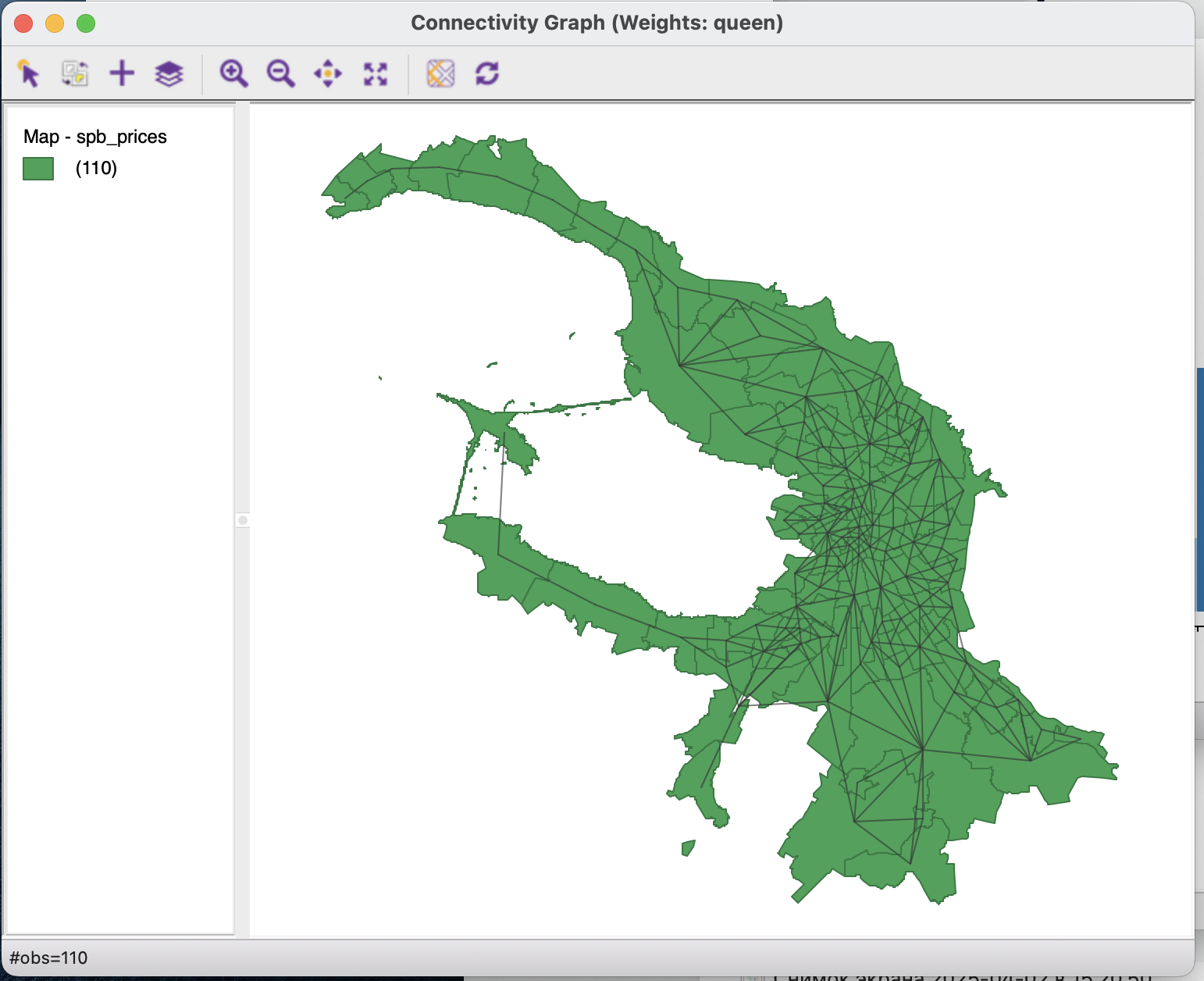
При выделении одного из объектов на графе будут отображаться только его соседи.
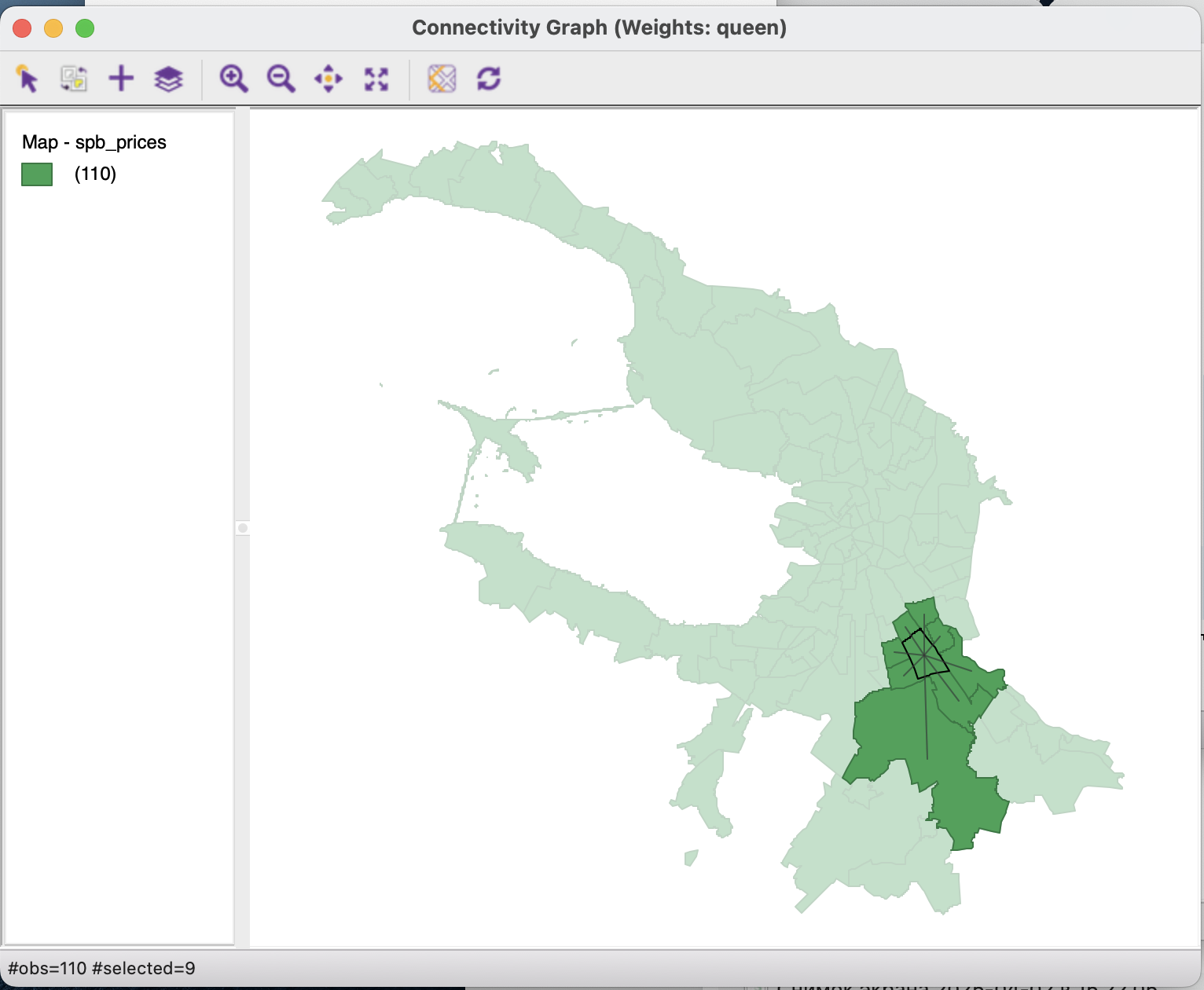
Если вы откроете матрицу пространственных весов в текстовом редакторе вы увидите только ее ненулевые элементы.

4.1.2 Принцип ладьи
Для того, чтобы объекты считались соседями, между ними должна быть общая ненулевая граница (то есть общей точки здесь недостаточно).
Построение матрицы весов по принципу ладьи происходит аналогично предыдущему пункту.
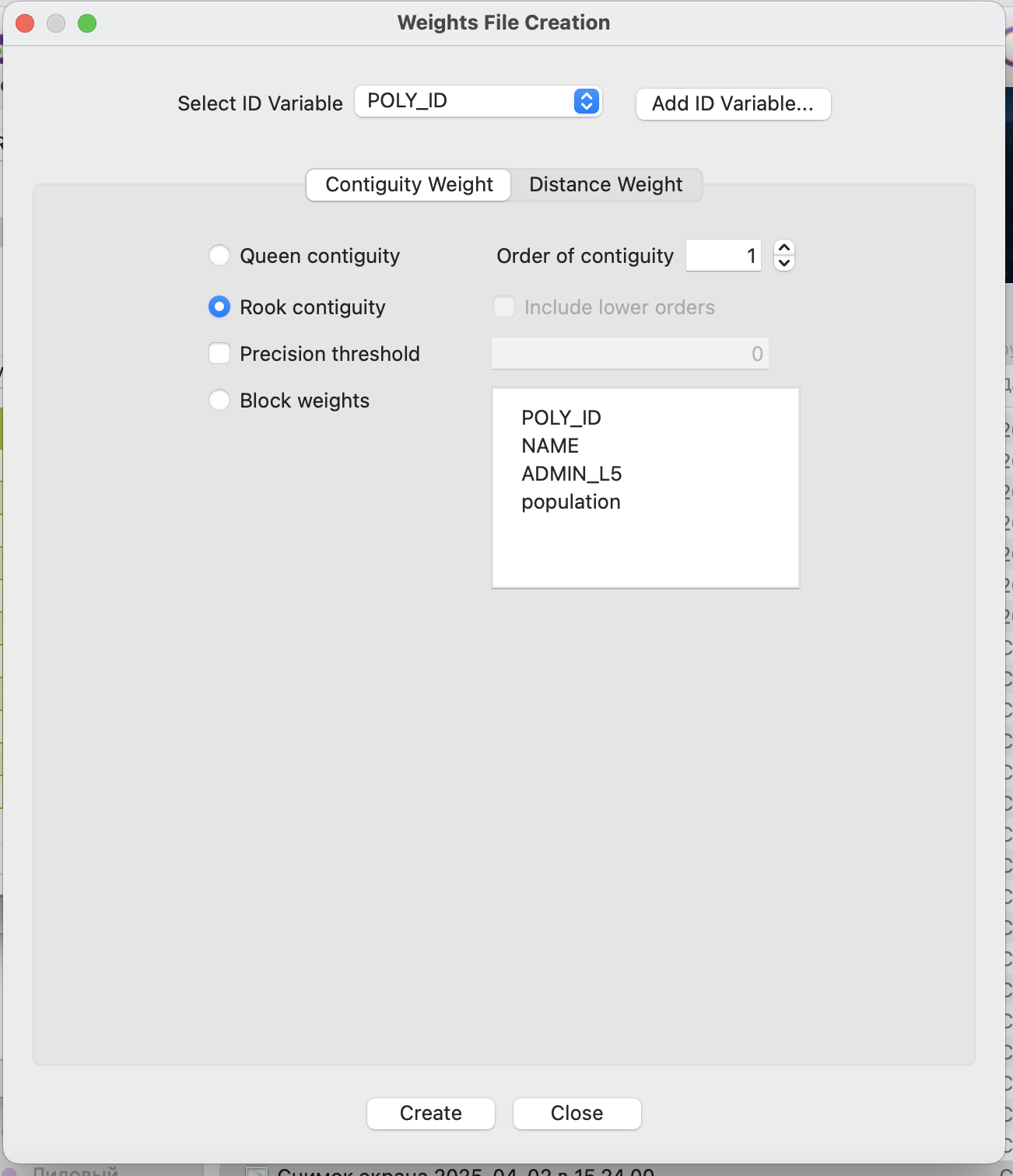
И после создания эта матрица также будет отображена в менеджере весов.
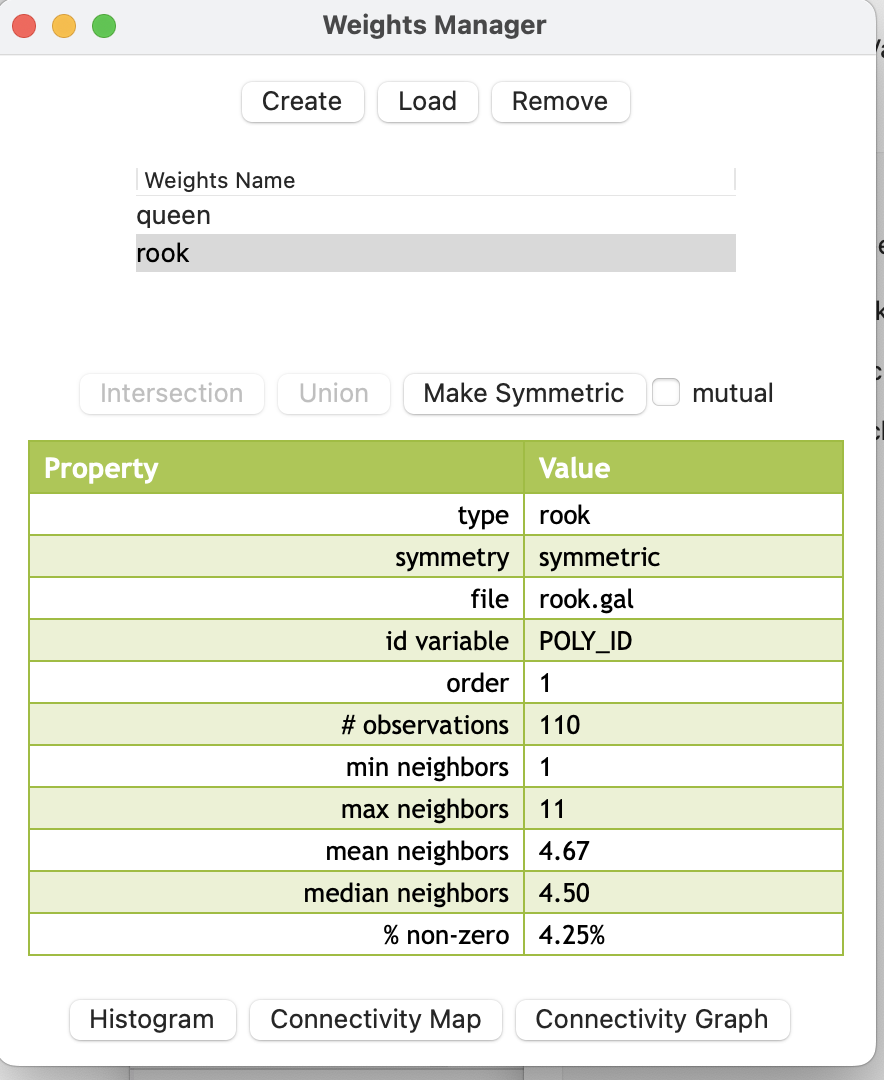
Аналогично матрице весов по принципу ферзя/королевы вы можете более подробно изучить структуру матрицы с помощью графиков:
- гистограмма;
- карта связности;
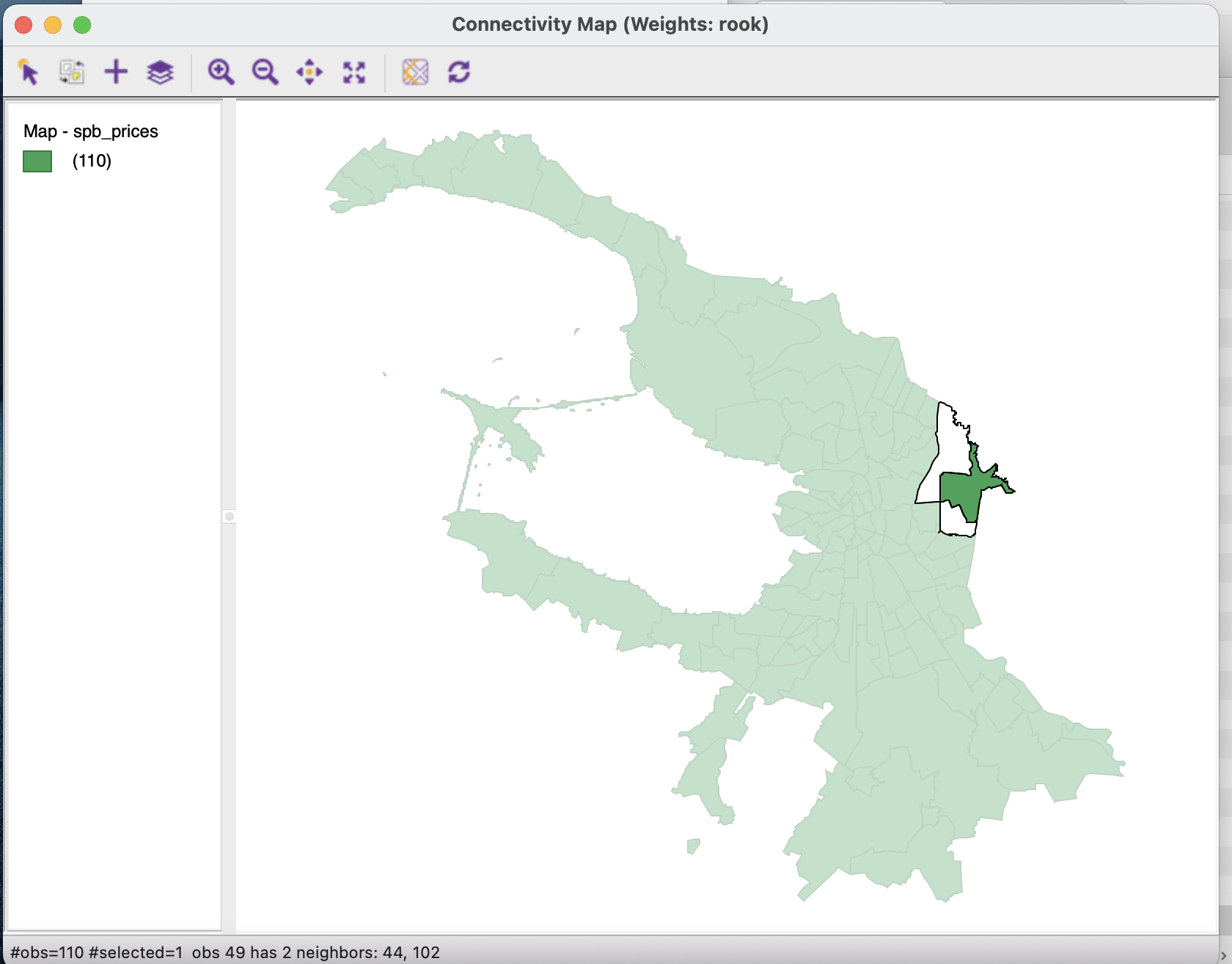
Обратите внимание, что в нижней панели окна карты связности отображается номер объекта, на котором расположен курсор и номера его соседей.
- граф связности.
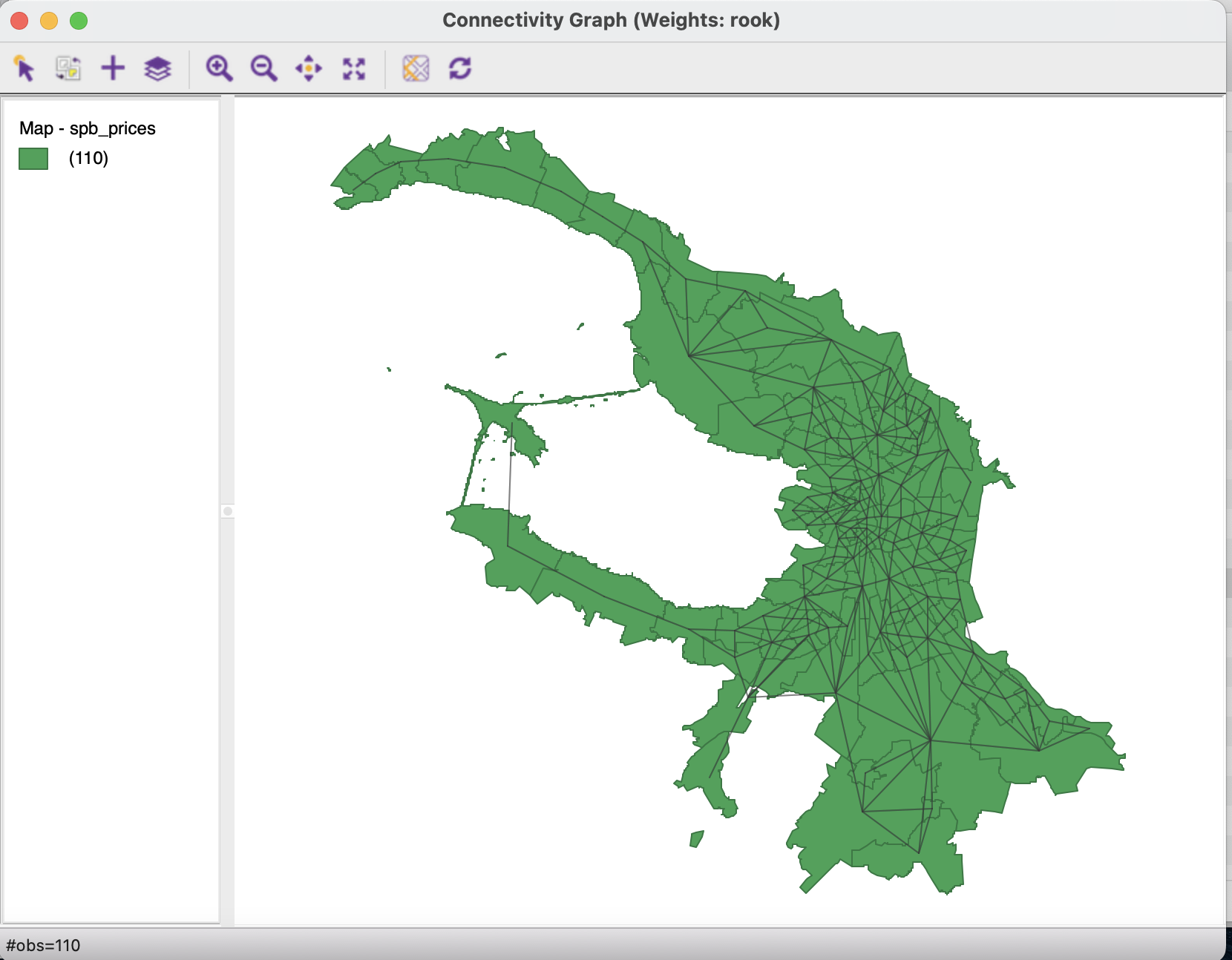
Обратите внимание, что при использовании принципа ладьи вы получаете в среднем меньше соседей для каждого из объектов.
Также вы можете попробовать определить соседей по смежности, используя QGIS.
Еще один вариант расчета ближайших соседей с использованием скрипта python для QGIS рассмотрен по ссылке.
Матрицы весов по смежности всегда будут симметричными относительно главной диагонали, что с точки зрения соседства значит, что объект \(i\) будет соседом объекту \(j\) и наоборот.
4.2 Расчет весов по расстоянию
При расчете весов по расстоянию необходимо задать значительно больше параметров.
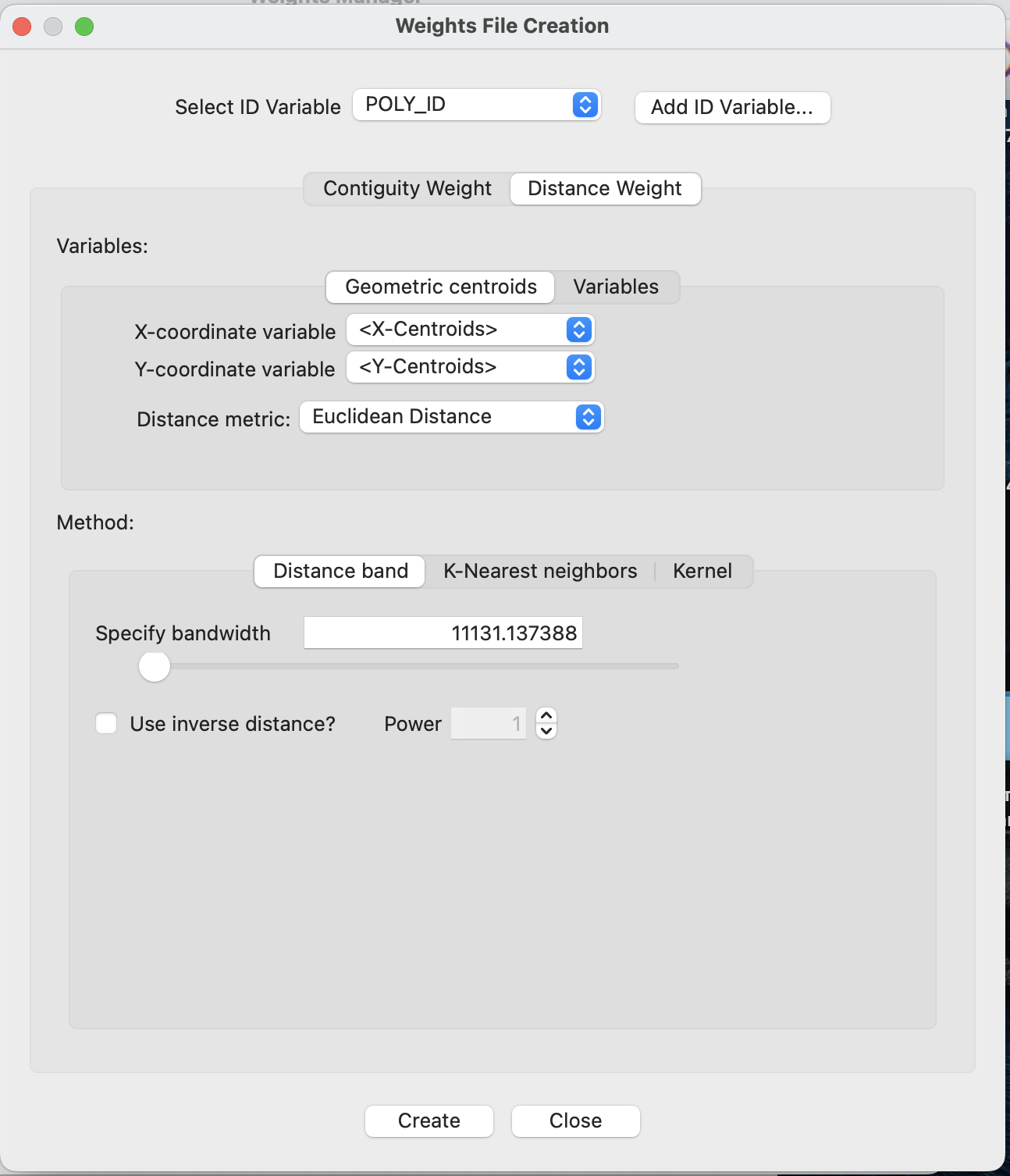
В первую очередь следует указать, как и между чем будет рассчитываеться расстояние.
По умолчанию для полигональных объектов предлагается использовать центроиды по координатам, но эти же центроиды могут рассчитываться по значениям любого числового показателя. Кроме того для расчета расстояния не обязательно вообще использовать центроиды или пространственное положение объектов, вы можете воспользоваться любыми числовыми показателями вашей атрибутивной таблицы.
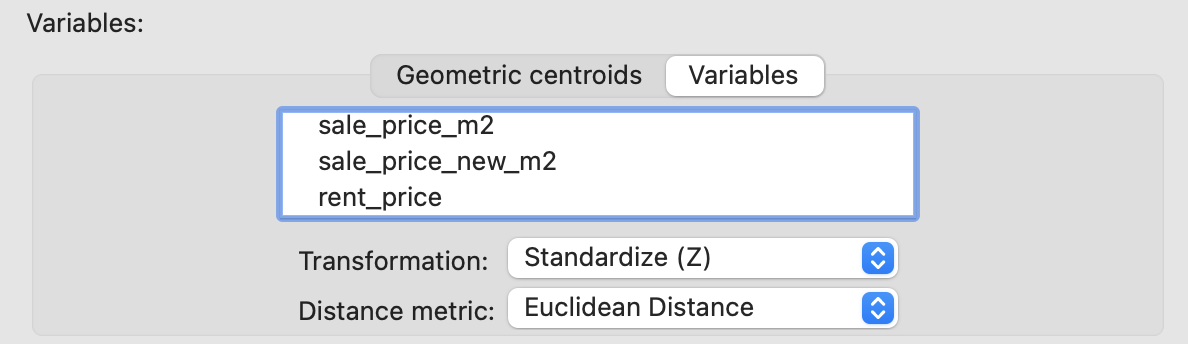
Расстояние может быть рассчитано двумя способами:
евклидово расстояние на плоскости;
расстояние на эллипсоиде (в милях или метрах).
Далее следует выбрать метод расчета весов по расстоянию и его параметры:
- distance band (гибридные веса) - объекты будут считаться соседями, если расстояние между ними не превышает заданного. Здесь в качестве параметра необходимо задать это расстояние, по умолчанию устанавливается такая величина расстояния, которая гарантирует всем объектам как минимум одного соседа (максимальное расстояние между ближайшими объектами).
Обратите внимание, что здесь вы можете использовать обратное расстояние (Inverse distance), то есть в результате в матрице весов будет исвользоваться не само расстояние, а \(\dfrac{1}{distance^{power}}\).
k-ближайших соседей, где необходимо задать необходимое число соседей;
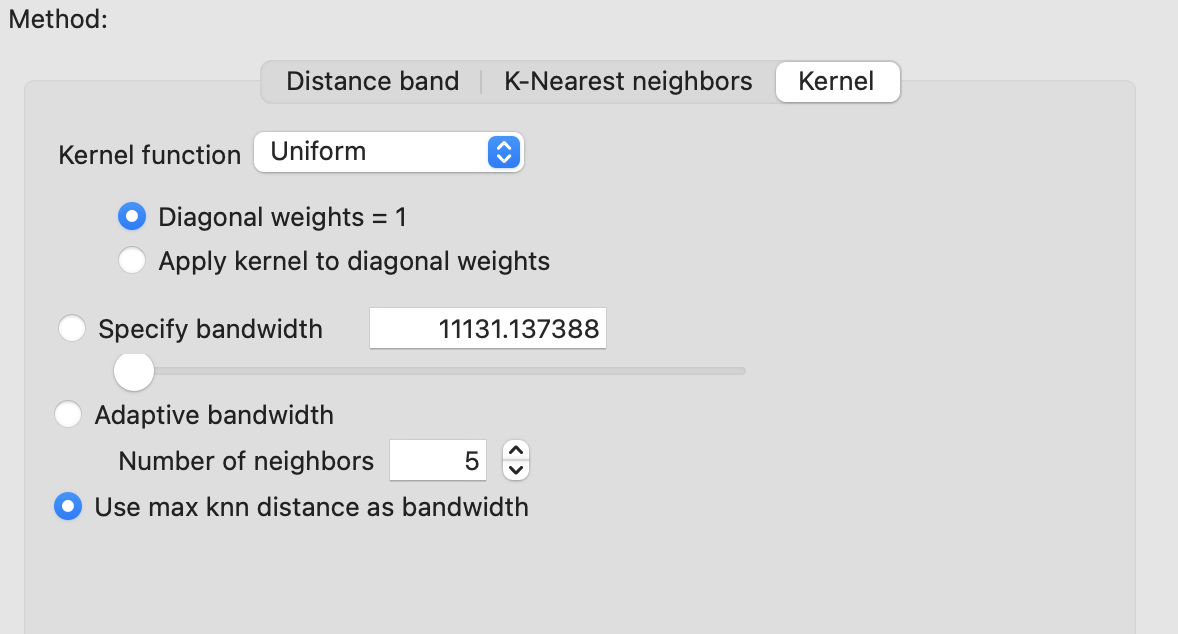
ядерные веса, для которых вы можете выбрать:
тип функции;
необходимость применения ее только в пределах определенного расстояния (specify bandwidth);
адаптивное расстояние, которое должно включать в себя определенное заданное число соседей;
возможность использовать максимальное расстояние для заданного числа соседей как ширину полосы пропускания.
В текстовом виде матрицы весов будут выглядеть иначе:
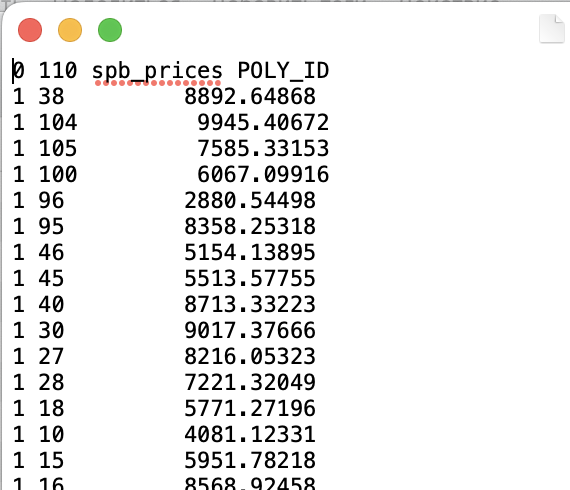

Здесь уже не будут просто перечислены ненулевые элементы, то есть список соседей для каждого объекта, а расстояние для каждой пары соседей: в случае гибридных весов и \(k\)-ближайших соседей - расстояние (то, которое было рассчитано), а в случае ядерных весов - значение ядерной функции от расстояния.
Попробуйте построить различные матрицы весов для разных параметров и сравнить их между собой.
Матрицы весов по расстоянию уже не будут симметричными, то есть объект \(i\) может быть соседом объекту \(j\), в то время как объект \(j\) не будет являться соседом объекту \(i\).